9 DE Weapons, Projectiles, Damage
By Professor Randall K. Nichols, Kansas State University
STUDENT OBJECTIVES
- To further understand the parameters of kinetic energy weapons design.
- To explore different types of projectiles and their common bases in the laws of physics and thermodynamics
- To study both the propagation of projectiles and interaction causing damage to the target.
INTRODUCTION
When we think of kinetic energy weapons, we think of the larger space devoted to directed energy weapons (DEW). Under this banner, high technology devices like lasers, microwaves, particle beams, EMP, rockets, and hypersonic missiles. In a subset of DEW, we find guns, mortars, catapults, crossbows, bullets, torpedoes, shape charges, and spears, to name a few. The common factor is kinetic energy. “Kinetic” comes from the Greek word “kinesis,” which means “to move.” (Nielsen, 2012)So, DEW – its energy is directed toward a target and intercepts a small fraction of the target’s surface area. What is now included in this classification are unmanned aircraft systems (drones) and unmanned underwater vehicles. They are perfect deployment vehicles for small-scale CBRNE weapons. The former is covered for the reader. The latter is covered in (Nichols & al., Unmanned Vehicle Systems, and Operations on Air, Sea, and Land, 2020) and (Nichols & Sincavage, Disruptive Technologies with Applications in Airline, Marine, and Defense Industries, 2021). In this chapter, we expand on chapter 8, fundamental concepts about KEW, discuss the propagation towards a target, preview the interaction with a target, and complete the mechanisms by which the target is damaged. We will discuss a variety of projectiles balls, bullets, shape charge explosives, and Tae Kwon Do strikes.
COMMON FRAMEWORK (Chapter 8 Recap)
Weapons may be understood as devices that deposit energy on targets. The energy that must be deposited to achieve a given level of damage is relatively insensitive to the type of weapon employed. Nuclear weapons may be characterized in terms of megatons, bullets in terms of muzzle velocity, and particle beams in terms of amperes of current. Still, when reduced to common units for the energy absorbed by the target, similar levels of damage are achieved at similar levels of energy deposited. (Nielsen, 2012)
FUNDAMENTALS OF KEW
Motion causes kinetic energy. Mathematically, the kinetic energy of an object having a mass of M and velocity of v is
K= ½ Mv2 Equation 9.1
Where M is in kg,
V is m/s
K is in Joules, J = kg m2s2
The object with greater mass at the same velocity would have more energy than less mass. An object moving at a greater velocity has more energy. An object is given kinetic energy when outside forces act upon it, doing work and accelerating. An object loses kinetic energy when it exerts forces and works on a second object. The energy lost from an object one can take the form of additional kinetic energy on the second object (car hitting a car); as heat or loss of energy; disruption of the second object, such as a bullet hitting a deer.
Kinetic energy is gained or lost when an object is accelerated according to Newton’s law:
F = Ma Equation 9.2
Where F = force in Newtons (MKS system)
M = mass in kg
A = acceleration in m/sec2
Force is a vector quantity with magnitude and direction. Both must be specified for a complete solution.[1]
Acceleration due to gravity is 9.80665 m/sec2. Gravity exerts a force on all objects, accelerating them towards the center’s center regardless of their direction of motion.
HUNTING WILD BOARS
Picture a hunter shooting a wild boar at 300 yards with a rifle that shoots 308 Barnes 175-grain LRX BT centerfire bullets. (Barnes, 2022) We can calculate the trajectory of this specific bullet by a sum of the forces on the bullet leaving the rifle. The bullet exits the rifle at velocity v (use fps) in a straight line and will continue until some other force acts upon it. The force of gravity drives the bullet down at a rate of 32.1741 ft/s2. Atmospheric drag induces a force opposite in direction to the bullet’s velocity. This force decelerates the object, reducing its velocity. The bullet takes on a curved path of a shorter range with gravity. We can calculate the kinetic energy by slide rule or cheat and use the manufacturing tables (Barnes, 2022). The latter tells us that the KE on target for 300 yards is 1731 FT-LBs,[2] Based on a muzzle velocity leaving at 2432 FPS and arriving at 300 yards of 2111 FPS. The rifle is zeroed in at 100 yards, so the trajectory (drop) is zero. However, at 300 yards, the drop is – 14.5 inches. This particular bullet has a Ballistic Coefficient of 0.521 (BC). BC of a bullet measures its ability to overcome air resistance in flight (drag force). A high BC means the bullet will slow down less. The normal range for bullets is 0.12 – 1.0 LB/in2 (kg/m2 in MKS). Good thing the boar is a large animal because the BC drop on the Barnes 175 gr 308 is significant and would require adjustments to the scope. Most scopes have adjustments in MOA for up-down drop and left-right windage. MOA means the minute of the angle measured in degrees, specifically 1/60 of a degree. One MOA is one inch at 100 yards (or 3 inches at 300 yards). These are calibrated in 1/8, ¼ or ½
increments. Since the drop is -14.5 inches, the up-down control (assume 1/4 increments) would require 3 in/full click x 4 = 12 inches (4 full clicks) + ¾ of a full click = 14.25. Assume wind = negligible and less than five mph. This also assumes the boar is polite enough not to move. The key takeaway is that the KE at 300 yards is 896 FT-LBs less than when it left the rifle’s muzzle.
It lost 34% of its rated energy to drag and gravity. BTW, wild boar skin is quite tough and has plenty of fat buildup. The 308 is a good choice for a wild boar under average conditions, from a mid-range distance, with a medium grain expanding bullet and correct shot placement. [3]
AT THE BOAR SKIN
The shielding thickness in older wild boars is approximately 2 inches thick. This very thick skin makes the wild boar resistant to holes. When a projectile encounters a target, our interest shifts from the forces felt by the projectile to those felt by the target. The forces are mirror imaging. Two principles come into play when evaluating the interaction between a KEW and its target. One is the conservation of energy, which says that energy is conserved. The energy lost from the projectile must be transferred (given to /picked up by) the target. If the bullet enters the target at one velocity and emerges from the other side with a lower velocity, the energy transferred to the target is the difference in the kinetic energies on entry and exit. In the case of a boar, the bullets enter the boar, slow down as it passes through 2 inches of tough skin, find their way to vital organs, and stop. The kinetic energy entering the skin is about 896 FT-LBs at 300 yards, and all of that energy is picked up by the boar. The exit velocity is zero. Assuming a heart or kidney shot, that is quite a punch. The loss of kinetic energy through the two inches of boar skin is a function of the drag coefficient, Cd, which is equal to the drag force D divided by the density ρ, times 1/2 the velocity, v squared time the reference area A. It expresses the ratio of drag force to the force produced by dynamic pressure times the area.
Fd = mg = D = ½ CdρAv2 Equation 9.3
Where:
A = m2 = (2in = 0.0508 m) = 0.00258 m2
Ρ =kg/m3 (use density of water at 997 kg/ m3 & not Air density of 1.21 kg/m3 )
M = kg = m-boar = 80 kg
g = 9.80 m/s2
Cd = 0.43
Eq 9.3 can be used to determine the difference in velocities in and out of the 2 inches of skin.
We can assume that the boar is as tough as a Dodge Ram pickup (in the field coming at you at 20 mph, you will think it is a tank or APC). The Cd is 0.43.
Fnet = mg – Fd = ½ CdρAv2 Equation 9.4
Where: v2 = (vin – vout )2 Equation 9.5
vnet = sqrt ( 2 mg / ρ Cd A) = sqrt [ 2 (80 kg) (9.80 m/ s2 ] / (997 kg /m3 ) 0.43) (0.00258 m2 )
vnet sqrt ( 1568 / 1.106) =sqrt ( 1417.72 ) = 37.65 m/ s2 net
The 308 hit the skin at 2118 FPS lost ~ 38 FPS through the skin = 2080 FPS into the organs. This loss of velocity is small based on the fluid density of water. Neither water nor air density coefficients are correct. They are merely range OM[4] identification/ approximations.[5] The actual density of boar skin & fat is unknown. A reasonable approximation of the loss of kinetic energy through the skin could be based on the BC. Therefore, 896 FT-LBs at 300 yards x 0.521 = 467 FT-LBs of kinetic energy. [6]
The second principle is the conservation of momentum. Momentum is calculated as the product of mass and velocity, Mv. Conservation of momentum requires that the total momentum of the bullet and target be the same before and after they interact. If the boar is initially at rest, and hit by the 308 bullets, with Mvo, the boar’s momentum and that of the bullet after the hit will sum to Mvo. Velocity is a vector quantity, so direction is important, as is magnitude.
DAMAGE
Rather than think in terms of gross features of velocity and energy, the boar experiences pain or damage. Damage is the internal disruption of a target. Physical damage of a target is determined by the pressure it feels, the area over which it is applied, and the time for which the pressure is applied. Pressure is the force the boar (target) feels, divided by the area over which that force is applied. (Nielsen, 2012) The target area over which pressure is applied is important. The total force felt by a target is the pressure applied multiplied by the area over which it is applied.
Practical self-defense example: [7] Against any two-handed push, the defender can step back and scoop downward and out, bringing the opponent’s torso down and forward. The defender carries the momentum of the scoop into the blow, directed to the ears with cupped hands. This technique can be executed (several times) with a K’ihap (short shout) in 7/10 of one second. The medical implications of this defense are significant: unconsciousness or a concussion, rupture of the tympanic membrane with intense pain, possible fracture or dislocation of the jaw, and contusion of the facial nerves and veins. (Adams, 1985) The damage is over a small area, the ear canals.
The time over which a force is also important in determining the target’s response. The force times the time over which the force is applied is known as Impulse. The key parameters for assessing target damage are momentum and energy of a KEW and resulting force, pressure, and Impulse. See Table 9.1
Table 9.1 Parameters affecting Target Response and Damage
| Parameter | Symbol | Units | Definition | Comment |
| Kinetic Energy | K | Joules (J) | Mv2 / 2 | Mv projectile mass, velocity |
| Momentum | ρ | kg m/sec | Mv | K and ρ are conserved when particles collide |
| Force | F | Newtons (Nt) | M dv/dt | F = dp/dt |
| Pressure | P | Nt/m2 | Force / Area | Force/ Area = Energy/ Volume (Nt/m2) |
| Impulse | I | Nt sec | Force x Time |
Source: Adapted from Table 2.1, p33 in (Nielsen, 2012)
SACRIFICIAL DRONES
Raytheon demonstrated the counter-drone capability of its Coyote Block 2+ drone in a newly released YouTube video at https://www.youtube.com/watch?v=RrRScxnDfrk&t=18s
, showing the unmanned vehicle blasting an unmanned aerial platform. (BISHT, 2022) See Figures 9.1 & 9.2. The Coyote is designed to take out small airborne targets.
The video shows the drone launch from a 4×4 Oshkosh Mine-resistant ambush-protected vehicle (M-ATV) and fixed palletized launch system, exploding just before contact with an incoming unmanned platform, destroying it mid-air. The video reveals that the M-ATV is linked to Ku-720 mobile sensing radars while the fixed launcher is fitted with KuRFS precision targeting radar. KuRFS uses multiple small antennas to “spot, locate, and track small targets at long range,” including incoming mortars, rockets, and drones. (BISHT, 2022)
Israel has been in a battle with Hezbollah for many years. Hezbollah has the nasty habit of shooting missiles over Israeli cities. Beyond the Iron Dome defenses, Israel counters with IAI Harop loitering munitions (drone). Developed by the MBT division of Israel Aerospace Industries, it is an anti-radiation drone that can autonomously home in on radio emissions. This SEAD-optimized[8] loitering munition is designed to loiter the battlefield and attack targets by self-destructing them. The drone can operate fully autonomously, using its anti-radar homing system, or work in a human-in-the-loop mode. If a target is not engaged, the drone will return and land itself back at base. It has been designed to minimize its radar signature through stealth (low-observability). This anti-radiation drone is designed to target enemy air-defense systems in the first line of attack. The small drone (with its small radar cross-section) can evade SAMs and radar detection systems designed to target much larger aircraft or intercept fixed-trajectory missiles.
The IAI Harop has a loiter (flying) time of 6 hours and a range of 1,000 km both ways. It is a larger version of the IAI Harpy and is launched from the ground- or sea-based canisters but can be adapted for air launch. The Harop can operate fully autonomously or take a man-in-the-loop mode, controlled by a remote operator. The Harop features two guidance modes: it can home in on radio emissions by itself with its anti-radar homing system, or the operator can select static or moving targets detected by the aircraft’s electro-optical sensor. This latter mode allows the HAROP to attack radars that are presently shut down, therefore not providing emissions for the aircraft to automatically home in on. If a target is not engaged, the drone will return and land itself back at base. See Figure 9.3. (Herzog, 2022)
Figure 9.1 Coyote Unmanned Aircraft System.

Source: Raytheon Missiles and Defense (BISHT, 2022)
Figure 9.2 Coyote unmanned aircraft system on the tarmac of Avon Park Air Force Range in Florida.

Source: Image: National Oceanic and Atmospheric Administration (BISHT, 2022)
Figure 9.3 IAI Israeli HAROP

Source: (Herzog, 2022) https://en.wikipedia.org/wiki/IAI_Harop#:~:text=By%20Julian%20Herzog%2C%20CC%20BY%204.0%2C%20https%3A//commons.wikimedia.org/w/index.php%3Fcurid%3D26893414
Sacrificial drones are examples of KEW against other drones or missiles. They propagate through the lower atmosphere. The earth’s atmosphere extends to an altitude no greater than 100 km. (62.137 miles = 328,084 ft). Depending on the class, UASs fly from 400 ft to 75,000 ft (0.1219 km – 30.48 km). The ceiling on the IAI Harop is 44,600 m = 15,000 ft. It is armed with a 51 LB = 23 kg warhead and travels at 417 km/h = 259 mph = 225 kn. Its range is 1000 km = 620 mi. It has a circular error probable (CEP), a measure of precision, < 1 m (3ft 3 in) with a 16 kg (35 LB) warhead.
PROPAGATION IN AN ATMOSPHERE
Kamikaze (suicide) drones are KEW in the atmosphere. They are so near to the surface of the earth we can assume that the force of gravity, F = GmM / r2, does not vary significantly for projectiles (whose flight is limited to altitudes within the earth’s atmosphere – our Kamikaze’s)
The Law of Universal Gravitation describes the effects of gravity on the motion of an object. In Eq 9.6,
F = GmM / r2 Equation 9.6
Where:
M & m are the masses of two bodies, kg
r is the distance separating them, m
G is the gravitational constant = 6.67 x 10-11 Nt m2 /kg2
F is the attractive force in nt.
The simpler form of this equation is F = mg, and the direction is towards the earth with an acceleration due to gravity = 9.8 m/sec2 in MKS units. (Nielsen, 2012)
Another assumption for low-level drone flight is that the earth’s curvature is negligible. Artillery rounds have an effective range of about 30 km. Bullets are normally VLOS. [9] 1000 yards is the effective limit. Ballistics is the study of projectile motion. The Barnes chart provides ballistic data out to 500 yards for calibers 223 Remington to 458 Winchester. (Barnes, 2022)
Hitting one drone with another is an exterior ballistics problem. It is not as hard as shooting a golf ball at an ICBM, but it does require some understanding of Propagation effects and damage caused by them.
SIR ISAAC NEWTON (1643-1727)
Newton’s three laws of motion explain the relationship between a physical object and the forces acting upon it. They are:
- 1) An object at rest remains at rest; an object in motion remains in motion at a constant speed and in a straight line unless acted on by an unbalanced force.
- 2) The acceleration of an object depends on the object’s mass and the amount of force applied.
- 3) Whenever one object exerts a force on another object, the second object exerts an equal and opposite on the first.
NEWTON’S FIRST LAW
Newton’s first law gave the concept of Inertia, or the tendency to resist changes in the state of motion. There is no net force acting on an object (if all the external forces cancel each other out). The object will maintain a constant velocity. If that velocity is zero, the object remains at rest. If external forces act on an object, the velocity will change because of the force. An example of Inertia involving aerodynamics is the motion of a killer drone changing the throttle setting of the engine to dive down on its target drone. (Glenn Research Center, 2022)
NEWTON’S SECOND LAW
Newton’s second law defines a force as equal to a change in momentum (mass times velocity) per change in time. Momentum is defined as the mass m of an object times its velocity V. Explore Figure 9.4.
Figure 9.4 Newtons Second Law of Motion Relationships

Source: (Glenn Research Center, 2022)
Let us assume that we have an unmanned airplane at a point “0” defined by its location X0 and time t0. The airplane has a mass of m0 and travels at a velocity of V0. An external force F to the airplane shown above moves it to point “1”. The unmanned airplane’s new location is X1 and time t1.
The mass and velocity of the airplane change during the flight to values m1 and V1. Newton’s second law can help us determine the new values of V1 and m1 if we know how big the force F is. Let us just take the difference between the conditions at point “1” and the conditions at point “0”.
F = (m1 * V1 – m0 * V0) / (t1 – t0 Equation 9.7
Newton’s second law talks about changes in momentum (m * V), so, at this point, we can’t separate how much the mass changed and how much the velocity changed. We only know how much product (m * V) changed.
Let us assume that the mass stays at a constant value equal to m. This assumption is good for an unmanned airplane; the only change in mass would be the fuel burned between point “1” and point “0”. The weight of the fuel is probably small relative to the weight of the rest of the airplane, especially if we only look at small changes in time. If we were discussing the flight of a baseball, then the mass remains a constant. But if we were discussing the flight of a bottle rocket, then the mass does not remain a constant, and we can only look at changes in momentum. For a constant mass m, Newton’s second law looks like this:
F = m * (V1 – V0) / (t1 – t0) Equation 9.8
The change in velocity divided by the change in time is the definition of the acceleration a. The second law then reduces to the more familiar product of a mass times acceleration:
F = m * a Equation 9.9
Remember that this relation is only good for objects with a constant mass. This equation tells us that an object subjected to an external force will accelerate and that the amount of the acceleration is proportional to the size of the force. The amount of acceleration is also inversely proportional to the object’s mass; for equal forces, a heavier object will experience less acceleration than a lighter object. Considering the momentum equation, a force causes a change in velocity; likewise, a change in velocity generates a force. The equation works both ways.
The velocity, force, acceleration, and momentum have both a magnitude and a direction associated with them. Scientists and mathematicians call this a vector quantity. The equations shown here are vector equations and can be applied in each component direction. We have only looked at one direction, and, in general, an object moves in all three directions (up-down, left-right, forward-back).
Example of force involving aerodynamics: An aircraft’s motion resulting from aerodynamic forces, aircraft weight, and thrust. (Glenn Research Center, 2022)
NEWTON’S THIRD LAW
Newton’s third law states whenever one object exerts a force on a second object; the second object exerts an equal and opposite force on the first. His third law states that for every action (force) in nature, there is an equal and opposite reaction. If object A exerts a force on object B, object B also exerts an equal and opposite force on object A. In other words, forces result from interactions. Examples of action and reaction involving aerodynamics: the motion of lift from an airfoil, the air is deflected downward by the airfoil’s action, and in reaction, the wing is pushed upward, or the motion of a jet engine produces thrust and hot exhaust gases flow out the back of the engine, and a thrusting force is produced in the opposite direction. (Glenn Research Center, 2022)
SHOOTING IN THE AIR
Let’s try to take down the UAS with a rifle bullet. This is analogous to solving Newton’s second law under the influence of gravity. The motion is broken down logically into two parts – in the downrange direction, denoted by z, and the up or down in altitude, denoted by h. There is a corresponding velocity downrange, vz, and rising to falling, vh. After the bullet is fired, at some time t, the bullet has propagated a distance z downstream and is at an altitude h above the earth’s surface. Refer to Figure 9.4. The bullets’ velocity, v, is two components: vz, the rate at which z is increasing, and vh, the rate at which h is increasing or decreasing. For vh positive, the bullet is rising, and for vh negative, the bullet is falling back to earth. [10] (Nielsen, 2012)
Equation 9.10 solves Newton’s law for vh, vz, h, and z when the force of gravity acts upon a bullet (projectile):
Vh = voh – gt
Vz = voz
H= voh * t – gt2 / 2
Z = voz *t Equation 9.10 (group)
Voh and voz are the bullet’s initial velocities in the h and z directions, respectively. Gravity does not affect vz, and the bullet moves downrange at a constant velocity, with z growing linearly in time. Vh steadily decreases in time due to gravity until it becomes negative and the bullet falls. The range of the bullet can be found by solving h for to at h=0. Plugging the answer back into the equation for z gives the result:
To = 2 voh / g and zr = 2 voh * vox / g (Nielsen, 2012)
The initial velocity components (voh, voz) determine the range of the bullet. They are not independent. The gun will release at a total muzzle velocity. This is broken down into voh and voz by setting the elevation angle of the launcher.
Figure 9.5 Projectile Distance and Velocity Coordinates
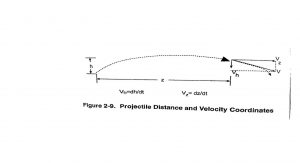
Source: Courtesy and Adapted from Figure 2-9 p46 in (Nielsen, 2012)
Figure 9.6 shows the effect of elevation angle on velocity components. At a given elevation angle, ϕ produces vertical and horizontal component vectors. At ϕ = 90o the shooter aims directly up and comes back down to the launch point. At ϕ = 45o, the maximum range is achieved. The shape and mass do not enter this analysis nor affect the propagation. (Nielsen, 2012)
DRONE VS DRONE IN AIR – COMPLEXITY
The bullet prorogation is a simple case to demonstrate forces on a projectile aimed at a target.
The picture is more complex when we have a suicide drone trying to intercept another drone. First, we need 3 – dimensional accurate position fixes in space (X, Y, Z ). Both drones are moving. So, the fixes are concerning time. The paths will have to be constantly updated with both feedback and feedforward information to align the drones for target damage. This can be done by radar or sonar pulses. The equations are second-order differential. We are constantly calculating the differentials and then integrating them back to identify the area of attacks and closure rates. They require onboard computing horsepower or offloading to the ground station and return signal interpretation. The computer has to calculate an accurate collision point. Normally we calculate the probable collision point to AVOID collision. In the Kamikaze scenario, we try to cut the distance to zero and make the collision happen. The target is not going to play nice in the sandbox. It detects the intruder and moves at extreme angles to avoid the pursuer. Another factor is AOA or angle of attack. Both drones will be using their AI and C3 systems to produce synchronous or asynchronous movements for attack and defense. It is a beautiful set of solutions to equations in real-time. [11] Think about shooting down an incoming missile with a nuclear MIRV warhead if you want to get a real sense of the mathematics’ difficulty. See / digest: (N & Blauwkamp, 2010)
Figure 9.6 Effect Of Elevation Angle On Velocity Components
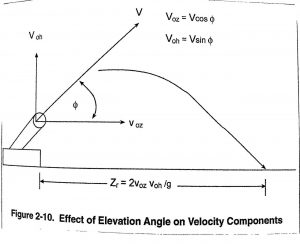
Source: Courtesy of and Adapted from Figure 2-10 p 47 in (Nielsen, 2012)
FLIGHT EQUATIONS WITH FORCES [12]
Refer to Figure 9.7 for the following discussion courtesy of Glenn Research Center.
Figure 9.7 Flight Equations with Drag
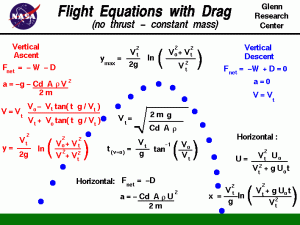
Source: Courtesy of (Glenn Research Center, 2022)
A ball in flight has no engine to produce thrust, so the resulting flight is similar to the flight of a shell from a cannon or a bullet from a gun. This type of flight is called ballistic flight and assumes that weight is the only force acting on the ball or bullet. In this section, we address the key equations which describe the motion of a flying ball or bullet, including the effects of drag. Full derivations are not provided as they can be found in the literature. (Glenn Research Center, 2022) The discussion centers around launching a ball into the air but refers to any projectile launched into a low earth atmosphere.
THRUST
Thrust is the force that moves an aircraft or UAS through the air. Thrust is used to overcome the drag of an airplane or UAS and to overcome the weight of a rocket. Thrust is generated by the engines of the aircraft or UAS through some kind of propulsion system. (NASA, 2022) See Figure 9.8
Figure 9.8 Thrust
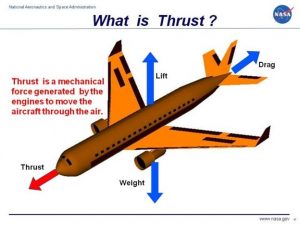
Source: courtesy of (NASA, 2022)
Vertical Location
At launch, the ball is inclined at some angle to the vertical, so we resolve the initial velocity into a vertical and horizontal component. Unlike the ballistic flight equations, the horizontal equation includes the action of aerodynamic drag on the ball. We first consider the vertical component and then develop the equations for the horizontal component.
In the vertical plane, the only forces acting on the ball are the forces of weight and drag. There is a characteristic velocity that appears in many of the equations. It is called the terminal velocity because it is the constant velocity the object sustains during a coasting descent. Terminal velocity is noted by the symbol Vt.
Vertical Descent
During the vertical descent, for a light object,[13] The weight and drag of an object are equal and opposite. There is no net force acting on the ball, and the vertical acceleration is zero.
a = 0
W = D
Where a is the acceleration, W is the weight, and D is the drag. The weight equation gives the weight of any object:
W = m * g
Where m is the mass of the object and g is the gravitational acceleration equal to 32.2 ft/sec^2 or 9.8 m/sec2 on the earth’s surface. The drag equation gives the drag:
D = .5 * Cd * ρ * A * Vt2 Equation 9.11
Where ρ is the gas density, Cd is the drag coefficient which characterizes the effects of the shape of the ball or bullet or projectile, A is the cross-sectional area of the ball, and Vt is the terminal velocity. [14] (Glenn Research Center, 2022)
Velocity
Terminal velocity is calculated:
Vt = sqrt ( (2 * m * g) / (Cd * ρ * A) ) Equation 9.12
Where: m * g = .5 * Cd * ρ * A * Vt2
Turning to the ascent trajectory, the ball travels at an initial vertical velocity Vo. With the positive vertical coordinate denoted by y, the net vertical force Fnet acting on the ball is given by:
Fnet = -W -D
Because the weight of the object is a constant, we can use the simple form of Newton’s second law to solve for the vertical acceleration:
Fnet = m * a = -W – D
m * a = – (m * g) – (.5 * Cd ρ * * A * v^2)
a = -g – (Cd * ρ * A * v2) / (2 * m)
Notice that the acceleration changes with time. Multiply the last term by g/g and use the definition of the terminal velocity to obtain:
a = -g * (1 + v2 / Vt2) Equation 9.13
Acceleration
The acceleration is the time rate of change of velocity:[15]
V/Vt = (Vo – Vt * tan(g * t / Vt)) / (Vt + Vo * tan (g * t / Vt)) Equation 9.14
Vertical Ascent
This is the equation for the velocity during the vertical ascent. At the top of the trajectory, the velocity is zero. We can solve the velocity equation to determine the time when this occurs:
Vo/Vt = tan(g * t(v=o) / Vt) and
t(v=o) = (Vt / g) * tan-1 (Vo/Vt)
so, y = (Vt^2 / (2 * g)) * ln ((Vo^2 + Vt^2)/(V^2 + Vt^2)) Equation 9.15
Notice that the location equation is pretty messy! For a given time t, we would have to find the local velocity V and then plug that value into the location equation to get the location y. At the maximum height ymax, the velocity is equal to zero:[16]
ymax = (Vt^2 / (2 * g)) * ln ((Vo^2 + Vt^2)/Vt^2) 9.16
Horizontal Location
The horizontal equations are a little less messy since the only net force acting on the ball is the drag:
Fnet = m a = – D Equation 9.17
The horizontal velocity is inversely dependent on the time. We can solve for the location x at any time by integrating the terminal velocity equation 9.12 to get:
x = (Vt2 / g) * ln( (Vt2 + g * Uo * t) / Vt2 ) Equation 9.18
SUMMARY: PROPAGATION IN THE ATMOSPHERE
We have bounced around between balls, bullets, UAS, aircraft, and projectiles in the lower atmosphere. Eighteen equations later, what have you found? Here are five takeaways:
- Gravity and drag are the main forces that affect the propagation of a projectile in the atmosphere. Since we are close to the earth, gravity is a constant and vectored downward to the earth. Drag opposes the forward motion of a projectile and is proportional to its area as viewed from the bow ( front), the density of air or fluid, and the square of its velocity.
- Without drag, a projectile will have a max range when launched at an elevation ϕ =45o. Drag reduces both the range and altitude achieved by a projectile launched at a given elevation angle.
- The drag coefficient is a constant of proportionality which measures how well streamlining has reduced the pressure of air on the bow (front) of the projectile. Projectiles moving at supersonic speeds exhibit greater drag coefficients.
- Winds blow projectiles off course, changing the equations by imparting latitude and longitude dependent forces. [17]
- Another reasonable deduction pertains to stability. Recall that buzz bombs over London during WWII were very unstable in their initial designs. It was Hanna Reitsch, Germany’s female ace test pilot, that solved the instability issues for the “flying bombs.” (Patton, 2022)Projectiles will be unstable and tumble in flight (or pull hard to the starboard or port sides) if the center of the pressure lies ahead of the center of gravity. Designs for projectiles include tail fins or spinning. This is not an isolated problem. The Japanese designers created finned torpedoes that could perform “ a feat like an acrobat high-diving in shallow water.” This was to overcome the aerial torpedoes plunging 150 feet before climbing back to an attack depth of 40 feet. (Pearl Harbor Thunderfish in the Sky Japan’s Type 91 Modification, 2015)
INTERACTION WITH TARGETS – DAMAGE
The projectile will strike its target after propagation through the lower atmosphere (maybe). A significant amount of the projectile’s kinetic energy will be transferred to the target ( Newton’s Third Law), damaging it! Some of the parameters to be considered to affect the probability of exceeding the threshold for damage are Pressure and Impulse, Angle of Attack, and Target Material and Shape.
Pressure and Impulse
Pressure is the force applied per unit area as the projectile strikes the target. Impulse is the integral of the force over time ( the force applied multiplied by the time for which it is applied). High pressure and high Impulse are more effective in damaging targets than low equivalents. How much pressure and Impulse a round delivers to a target depends upon its KE, shape, and material. (Nielsen, 2012) Later in the chapter, we will look at the theory of Shaped Charges and how they can be used to destroy tanks or blow-up rock formations and promote commercial drilling operations. (Clipii, 2022) (Shekhar, 2012)
The Angle of Attack (AoA)
A glancing blow will deliver less punch than a direct one. The angle with which the projectile strikes a target is important in determining the effectiveness of the attack and the response of both the projectile and target. At a high AoA, the bullet may ricochet and have little effect, but at a low AoA, the bullet may cause severe damage. (Nielsen, 2012)
Target Material and Shape
The material and shape of a projectile will affect the pressure and Impulse it delivers; the material and shape of the target will affect its response.
All three of these factors can be seen as a practical demonstration. In Tae Kwon Do,[18] [19]students learn the Theory of Power to defend themselves:
- Concentration
- Reaction – Force
- Breathing Control
- Balance
- Speed
They are essentially combining the penetration factors of Pressure, Impulse, AoA, and knowledge of the Target to affect a turbulent defense of life. (Nichols R. K., Self Defense Concepts by U-Dan-Ja-Nim Randy Nichols, 3rd Dan (R), 2003)[20]
Figure 9.9 demonstrates the application of the Theory of Power and the Principles of KEW.
Figure 9.9 Smashing two Bricks without spacers for 2nd Degree Black Belt Test

Source: (Nichols R. K., 2nd Degree Black Belt Test – Decided)
Look closely at neck muscles and concrete splatter as the palm heal attack violently breaks the two hard concrete blocks. That’s pressure and a perfect AoA. From Table 9.2, the energy of penetration required for striking the solar plexus of an unprotected man is 80 Joules. Figure 9.8 shows two bricks at ~2 inches thick /each placed together (no air space). The energy being generated to penetrate the bricks is (4 inches = 10.16 centimeters) / 0.5 cm @ 1500 Joules = 30,400 Joules. The energy generated breaks the concrete blocks (target) over a concentrated area of attack about the size of ~ 1 in x 3 in the palm heal surface of the right hand.
Table 9.2 Kinetic Energy Required for a 7.62 mm Projectile to Penetrate Targets.
| Target Type | Energy for Penetration (Joules) |
| Unprotected Man | 80 |
| 23 cm Timber | 200 |
| Very light armor | 770 |
| 0.5 cm concrete | 1500 |
| 1.2 cm Brick | 3000 |
| 4 inches Concrete Blocks (no spacers) | 30,400 |
Sources: (Nielsen, 2012) (Nichols R. K., Self Defense Concepts by U-Dan-Ja-Nim Randy Nichols, 3rd Dan (R), 2003)
WHAT IS DAMAGE?
Given the three parameters that affect damage (Pressure and Impulse, Angle of Attack, and Target Material and Shape), what is the optimum way to combine these parameters to achieve a given level of damage? There are at least three possible effects of kinetic energy projectiles’ These are shown in Figure 9.10 They are penetration (going through the surface and rattling around for internal damage), fragmentation (shattering the target material and the projectile), and spallation (although penetration is not accomplished, the shock waves will propagate through the target and throw flakes of material off the back surface. (Nielsen, 2012) Predicting exactly the effects of kinetic energy projectiles on target composition and shape is complex and beyond the scope of this chapter. [21] [22]
Figure 9.10 Possible Effects Of Kinetic Energy Projectiles
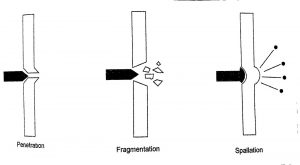
Source: Adapted from Figure 2-18 p61 in (Nielsen 2012)
SABOT PROJECTILE DESIGN
Figure 9.11 shows the Sabot APFSDS (Armor-piercing fin-stabilized discarding sabot) projectile. The modern projectile design uses projectiles that change their configuration during the different phases of their operation. This makes the target interaction optimal. The Sabot round is armor-piercing. The projectile has features designed for each flight portion from tube to target. (Nielsen, 2012)
The function of a sabot is to provide a larger bulkhead structure that fills the entire bore area between an intentionally designed sub-caliber flight projectile and the barrel, giving a larger surface area for propellant gasses to act upon than just the base of the smaller flight projectile. The efficient aerodynamic design of a flight projectile does not always accommodate the efficient interior ballistic design to achieve high muzzle velocity. This is especially true for arrow-type projectiles, which are long and thin for low drag efficiency but too thin to shoot from a gun barrel of equal diameter to achieve high muzzle velocity. The physics of interior ballistics demonstrates why a sabot is advantageous to achieving higher muzzle velocity with an arrow-type projectile. Propellant gasses generate high pressure, and the larger the base area that pressure acts upon, the greater the net force on that surface. Force (pressure times area) provides acceleration to the projectile’s mass. Therefore, a lighter projectile can be driven from a barrel to a higher muzzle velocity than a heavier projectile for a given pressure and barrel diameter. However, a lighter projectile may not fit in the barrel because it is too thin. To make up for this difference in diameter, a properly designed sabot provides less parasitic mass than if the flight projectile were made full-bore, in particular providing dramatic improvement in muzzle velocity for APDS (Armor-piercing discarding sabot) and APFSDS ammunition. (Bednarik, 2022)
Figure 9.11 SABOT APFSDS Projectile
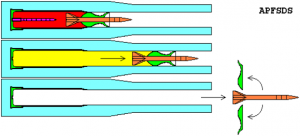
The function of an APFSDS sabot (Armor-piercing fin-stabilized discarding sabot)
red: propellant
orange: long rod penetrator
yellow: propellant gases
green: sabot
blue: gun barrel
Source: (Bednarik, 2022)
Shaped Charges [23]
One last item to be covered is the versatility of projectile design. One of the most useful designs is the shaped charge used in military and non-military applications.
A shaped charge is an explosive charge shaped to focus the effect of the explosive’s energy. Different types of shaped charges are used for various purposes such as cutting and forming metal, initiating nuclear weapons, penetrating armor, or perforating wells in the oil and gas industry.
A typical modern shaped charge, with a metal liner on the charge cavity, can penetrate armor steel to a depth of seven or more times the diameter of the charge (charge diameters, CD), though greater depths of 10 CD and above have been achieved. Contrary to a widespread misconception (possibly resulting from the acronym HEAT, short for high-explosive anti-tank), the shaped charge does not depend in any way on heating or melting for its effectiveness; that is, the jet from a shaped charge does not melt its way through armor, as its effect is purely kinetic – however, the process does create significant heat and often has a significant secondary incendiary effect after penetration. (Wikipedia, 2022)
Modern military
The common term in military terminology for shaped-charge warhead is high-explosive anti-tank warhead (HEAT). HEAT warheads are frequently used in anti-tank guided missiles, unguided rockets, gun-fired projectiles (both spun and unspun), rifle grenades, land mines, bomblets, torpedoes, and various other weapons. (Wikipedia, 2022) See Figure 9.12 for a HEAT example.
Figure 9.12 HEAT Projectile

Source: (Wikipedia, 2022)
Non-military
In non-military applications, shaped charges are used in the explosive demolition of buildings and structures, particularly for cutting through metal piles, columns, beams, and boring holes. In steelmaking, small, shaped charges are often used to pierce taps that have become plugged with slag. They are also used in quarrying, breaking up ice, breaking log jams, felling trees, and drilling post holes. Shaped charges are used most extensively in the petroleum and natural gas industries, particularly in completing oil and gas wells. They are detonated to perforate the well’s metal casing at intervals to admit the influx of oil and gas.
SHAPE CHARGE FUNCTIONS
A typical device consists of a solid explosive cylinder with a metal-lined conical hollow in one end and a central detonator, array of detonators, or detonation waveguide at the other end. Explosive energy is released directly away from (normal to) the surface of an explosive, so shaping the explosive will concentrate the explosive energy in the void. If the hollow is properly shaped (usually conically), the enormous pressure generated by the detonation of the explosive drives the liner in the hollow cavity inward to collapse upon its central axis. The resulting collision forms and projects a high-velocity jet of metal particles forward along the axis. Most of the jet material originates from the innermost part of the liner, a layer of about 10% to 20% of the thickness. The rest of the liner forms a slower-moving slug of material, which is sometimes called a “carrot” because of its appearance. (Wikipedia, 2022)
Because of the variation and the liner’s collapse velocity, the jet’s velocity also varies along its length, decreasing from the front. This variation in jet velocity stretches it and eventually breaks it into particles. Over time, the particles tend to fall out of alignment, which reduces the depth of penetration at long standoffs. (Wikipedia, 2022)
At the cone’s apex, which forms the very front of the jet, the liner does not have time to be fully accelerated before it forms its part. This results in its small part of the jet being projected at a lower velocity than the jet formed later behind it. As a result, the initial parts of the jet merge to form a pronounced wider tip portion. (Wikipedia, 2022)
Most of the jet travels at hypersonic speed. The tip moves at 7 to 14 km/s, the jet tail at a lower velocity (1 to 3 km/s), and the slug at a still lower velocity (less than 1 km/s). The exact velocities depend on the charge’s configuration and confinement, explosive type, materials used, and the explosive-initiation mode. At typical velocities, the penetration process generates such enormous pressure that it is considered hydrodynamic. (Wikipedia, 2022)
The location of the charge relative to its target is critical for optimum penetration for two reasons. If the charge is detonated too close, there is not enough time for the jet to fully develop. But the jet disintegrates and disperses after a relatively short distance, usually well under two meters. At such standoffs, it breaks into particles that tend to tumble and drift off the axis of penetration so that the successive particles tend to widen rather than deepen the hole. At very long standoffs, velocity is lost to air drag, further degrading penetration. (Wikipedia, 2022)
The key to the effectiveness of the hollow charge is its diameter. As the penetration continues through the target, the width of the hole decreases, leading to a characteristic “fist to finger” action, where the size of the eventual “finger” is based on the size of the original “fist.” In general, shaped charges can penetrate a steel plate as thick as 150% to 700%[44] of their diameter, depending on the charge quality. Figure 9.13 is for basic steel plate, not for the composite armor, reactive armor, or other types of modern armor. (Wikipedia, 2022)
Figure 9.13 shows the internals of the Shaped Charge Projectile.
Figure 9.13 Charge Projectile Detail
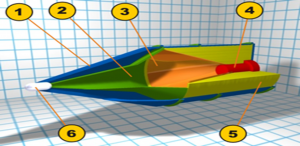
Source: (Wikipedia, 2022)
SUMMARY: TARGET INTERACTION
- Unlike propagation, which follows some clean physical laws, interaction is messy and highly scenario dependent. The effect of a projectile striking a target will depend on such weapon parameters as momentum, energy, and shape; such target parameters as material, thickness, and construction; and scenario parameters as AoA between the projectile and target.
- The target’s response is determined by the stress applied to it and the resulting strain or deformation it suffers. Both stress and strain are related mathematically to pressure and impulse.
- Projectile design involves tradeoffs among factors that influence acceleration, propagation, and interaction. (Nielsen, 2012)
Bibliography
Adams, B. (1985). Deadly Karate Blows The Medical Implications. Burbank, CA: Unique Publications.
Adamy, D. -0. (2015). EW 104 EW Against a New Generation of Threats. Boston: Artech House.
Adamy, D. (2001). EW 101 A First Course in Electronic Warfare. Boston, MA: Artech House.
Adamy, D. (2009). EW 103 Tactical Battlefield Communications Electronic Warfare. Boston, MA: Artech House.
Adamy, D. L. (2004). EW 102 A Second Course in Electronic Warfare. Boston: Artech House.
Barnes. (2022, February 19). Barnes Master Ballistics Charts- Rev 2021-03-23. Retrieved from www.barnesbullets.com: www.barnesbullets.com
Beason, D. (2005). The E-Bomb: How America’s new directed energy weapons will change the way future wars will be fought. Cambridge, MA: Da Capo Press.
Bednarik, K. (2022, February 20). Sabot Projectile. Retrieved from https://commons.wikimedia.org/: By The original uploader was Karl Bednarik at German Wikipedia. – Trhttps://commons.wikimedia.org/w/index.php?curid=4071358
BISHT, I. S. (2022, January 12). Raytheon-coyote-destroys-drone/. Retrieved from https://www.thedefensepost.com: https://www.thedefensepost.com/2022/01/12/raytheon-coyote-destroys-drone/
Clipii, T. (2022, February 20). On mathematical Modeling of Shaped Charge Penetration. Retrieved from http://www.diva-portal.org/: http://www.diva-portal.org/smash/get/diva2:18367/FULLTEXT01.pdf
Foley, W. S. (March 1979). Ancient Catapults. Scientific American, 240, 150.
Glasstone, S. &. (1977). The Effects of Nuclear Weapons, 3rd Edition. In S. &. Glasstone, Chapter V, Figures 5.20, 5.22 & 5.23. Washington, DC: UGPO.
Glenn Research Center. (2022, February 20). flight-equations-with-drag/. Retrieved from https://www1.grc.nasa.gov/: https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/flight-equations-with-drag/
Glenn Research Center. (2022, February 20). Newtons Three Laws of Motion. Retrieved from https://www1.grc.nasa.gov/: https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/newtons-laws-of-motion/
Halsam, C. M.-S. (1982). Small Arms and Cannons. Oxford: Brassey’s Publishers.
Herzog, B. J. (2022, February 19). IAI HAROP. Retrieved from https://commons.wikimedia.org: https://commons.wikimedia.org/w/index.php?curid=26893414
N, F. P., & Blauwkamp, R. &. (2010, January 29). Modern Homing Missile Guidance Theory and Techniques. Retrieved from https://www.jhuapl.edu/Content/techdigest/pdf/V29-N01/29-01-Palumbo_Homing.pdf: https://www.jhuapl.edu/Content/techdigest/pdf/V29-N01/29-01-Palumbo_Homing.pdf
NASA. (2022, February 20). Simple Forces on an Aircraft or UAS. Retrieved from https://www.grc.nasa.gov/WWW/K-12/airplane/thrust1.html: https://www.grc.nasa.gov/WWW/K-12/airplane/thrust1.html
Nichols, R. K. (2003). Self Defense Concepts by U-Dan-Ja-Nim Randy Nichols, 3rd Dan (R). Quantico, VA: INFOSEC Technologies.
Nichols, R. K. (2021). Chapter 14: Maritime Cybersecurity. In R. K. Nichols, & J. J. Ryan, Unmanned Vehicle Systems & Operations on Air, Sea, Land (pp. 330-356). Manhattan, KS: New Prairie Press #35.
Nichols, R. K. (2022). Chapter 18: Cybersecurity Counter Unmanned Aircraft Systems (C-UAS) and Artificial Intelligence. In D. M. R. K. Barnhart, Introduction to Unmanned Aircraft Systems, 3rd Edition (pp. 399-440). Boca Raton, FL: CRC.
Nichols, R. K. (n.d.). 2nd Degree Black Belt Test – Decided. Chois Tae Kwon Do School, Corpus Christi, TX.
Nichols, R. K., & Mumm, H. C. (2019). Unmanned Aircraft Systems in the Cyber Domain, 2nd Edition. Manhattan, KS: www.newprairiepress.org/ebooks/27.
Nichols, R. K., & Sincavage, S. M. (2021). Disruptive Technologies with Applications in Airline, Marine, and Defense Industries. Manhattan, KS: New Prairie Press #38.
Nichols, R. K., Mumm, H. C., Lonstein, W. D., Ryan, J. J., Carter, C., & and Hood, J.-P. (2019). Unmanned Aircraft Systems in the Cyber Domain, 2nd Edition. Manhattan, KS: NPP eBooks. 27. Retrieved from www.newprairiepress.org/ebooks/27
Nichols, R., & al., e. (2020). Unmanned Vehicle Systems and Operations on Air, Sea, and Land. Manhattan, KS: New Prairie Press #35.
Nichols, R., & Ryan, J. M. (2020). Unmanned Vehicle Systems & Operations on Air, Sea & Land. Manhattan, KS: New Prairie Press #35.
Nielsen, P. E. (2012). Effects of Directed Energy Weapons. Middletown, DE: CreateSpace Independent Publishing Platform.
Patton, R. E. (2022, February 20). Hanna-reitsch-Hitlers-female-test-pilot.htm. Retrieved from https://www.historynet.com/: https://www.historynet.com/hanna-reitsch-hitlers-female-test-pilot.htm
Pearl Harbor Thunderfish in the Sky Japan’s Type 91 Modification. (2015, December 28). Retrieved from https://www.pearlharboravaitionmuseum.org: https://www.pearlharboravaitionmuseum.org
Shekhar, H. (2012, September 2). Theoretical Modelling of Shaped Charges in the Last Two Decades (1990-2010): A Review. Retrieved from https://ipo.lukasiewicz.gov.pl/wydawnictwa/wp-content/uploads/2021/03/Shekhar2-2.pdf: https://ipo.lukasiewicz.gov.pl/wydawnictwa/wp-content/uploads/2021/03/Shekhar2-2.pdf
Vernard Foley, G. P. (January 1985). The Crossbow. Scientific American, 252, 104.
Wikipedia. (2022, February 20). Shaped_charge. Retrieved from https://en.wikipedia.org/wiki/: https://en.wikipedia.org/wiki/Shaped_charge
[1] In English units, v = fps; m=gr (convert to pounds, lb); KE = FT-LB; trajectory is in in; Ballistic coefficient, unitless
[2] The energy at the muzzle leaving is 2627 FT-LBs (Barnes, 2022)
[3] Author experience while on safari in India.
[4] OM = Order of Magnitude approximation
[5] The highest density range would be pure air and the lowest would-be pure water. Boar skin and fat density should be between these two values because the boar fluids combine with additional solids to change the density factor.
[6] Staring a wild boar down as it moves through the brush with you as his dinner in his mind, these calculations have little interest. Breathing, keeping the scope on the target, squeeze, center mass, one-shot, stance, training, be ready to jump into the APC vehicle if you miss – these are the mental calculations made.
[7] The author is a 3rd Dan Black Belt in Tae Kwon Do Moo Duk Kwan style. He previously taught self-defense courses.
[8] (SEAD = Suppression of Enemy Defenses)
[9] VLOS = visual line of sight. You need to be a marine or army snipe to take on a target above 1000 yards.
[10] Surprisingly, terrorists who shoot their AK-47s into the air haven’t studied this principle of gravity and change in height. With due respect, the gene pool of the group might be affected.
[11] Although fascinating, the required mathematics is out of the scope of this chapter. Be aware that the problem is quite complex; however, several firms have solved it and deployed their solutions in real-time.
[12] This section is taken from (Glenn Research Center, 2022) with grateful thanks from the author.
[13] Both UAS and bullets fit this assumption.
[14] NASA and Glenn Research Center seem to have some affinity for a “ball” discussion as a projectile; however, the equations fit almost any projectile, bullet, missile, or Kamikaze drone.
[15] Integration and substitutions in this derivation are left for the student to read (Glenn Research Center, 2022)
[16] See for a full messy discussion (Glenn Research Center, 2022)
[17] Although not specifically discussed, the effects are reasonable. See: (Nielsen 2012)
[18] Tae Kwon Do (TKD) means Tae – To jump, kick, or smash with the foot; Kwon – To punch or destroy with the hand or the fist; Do – The way or the method.
[19] The author is a 3rd Dan Black Belt (R). He taught self-defense courses for women and private students. At the peak of his career, he was honored to be elevated to ring judge in the TKD Nationals in San Antonio, TX.
[20] This Self Defense presentation(PPTX) is available free to readers, request from the author at profrknichols@ksu.edu.
[21] (Nielsen 2012) does discuss the subject; however, there is plenty of advanced research to be studied. Recommend contacting your local or educational library to access the many databases and papers.
[22] Since Chapter 12 is devoted to hyper-sonics or hypervelocity impacts ( velocities well in excess of the speed of sound), this topic is tabled.
[23] Wikipedia provides 85 references on the subject of Shaped Charges. Good start.

