8 DEW Primer
By Professor Randall K. Nichols, Kansas State University
Student Objectives
- To study the basic principles for Directed Energy Weapons (DEW)
- To recognize that DEWs can be launched from ground or air against CBRN assets or UAS / UUV
- To understand energy propagation and interaction are key elements in the analysis of weapons utility,
- To understand the common framework for DEW analysis, which is mostly insensitive to the weapon type,
- To look at how a DEW deposits energy in a target and then considers energy deposition and loss rates to determine the criteria for damaging the target.
INTRODUCTION[1]
This chapter is about the effects of directed energy weapons (DEW). We are interested in how they propagate to and interact with targets. Propagation and targe interaction are the key elements in analyzing a weapon’s utility to accomplish a given mission. The yield of its warhead determines the effectiveness of a nuclear missile and the accuracy of its guidance. The effectiveness of a rifle is determined by the type of round fired, the range to target, and the skill of the shooter who fires it. DEW weapons are no different. (Nielsen, 2012)[2]
In this textbook, the authors recognize that unmanned aircraft or underwater vehicles (UAS / UUV) are capable deployment agents for weapons (DEW included) – especially against CBRN assets and facilities or hostile airborne or underwater assets. (Nichols & Sincavage, 2021) This chapter is a primer on DEW effects. It sets the stage for the next five chapters in our book: Chapter 9: Kinetic Energy Weapons, Chapter 10: Lasers, Chapter 11: Microwaves, Chapter 12: Hypersonic Drones, and Chapter 13: Acoustic Weapons and Piracy. Chapters 14: Satellite Killers and Chapter 15: Cyber Weapons and CBRNE are special cases.
Weapons are devices that deliver sufficient energy to targets to damage them. Effective design requires a knowledge of the weapons and their characteristics. (Nielsen, 2012) Designers create the means of projecting energy onto the targets that planners choose to destroy. Weaponry is not a precise science. Propagation paths and target details are never known precisely. Using a 22 caliber against a bear might penetrate the skin (precisely) until you find a beer-bellied bear with thick full skin sitting around his cave watching TV to wait out the winter. This operational scenario might invalidate the precise calculations by the designer for weapon energy propagation.
COMMON FRAMEWORK
Weapons may be understood as devices that deposit energy on targets. The energy that must be deposited to achieve a given level of damage is relatively insensitive to the type of weapon employed. Nuclear weapons may be characterized in terms of megatons, bullets in terms of muzzle velocity, and particle beams in terms of amperes of current. Still, when reduced to common units for the energy absorbed by the target, similar levels of damage are achieved at similar levels of energy deposited. (Nielsen, 2012)
EFFECTS OF DIRECTED ENERGY WEAPONS (DEW)
Directed energy weapons make up various weapons such as lasers, particle beams, microwaves, and even bullets. All DEW are just devices that deposit energy in targets. That energy that must be deposited to achieve a given level of damage is relatively insensitive to the type of weapon employed. (Nielsen, 2012)[3] American DE weapons may change the way future wars will be fought. (Beason, 2005)
Energy cannot be deposited in a target unless it is first delivered to the target. This delivery mechanism is called the propagation of energy. This subject was covered in (Adamy D. 2001) (Adamy D., 2009) and (Nichols et al., 2019). There is always some loss of energy during propagation. The DEW must deliver more energy than needed to damage the target to compensate for the loss along the way. DE weapon design depends on the anticipated target, determining the energy required for damage. Second, the anticipated scenario (range, environment, time, etc. See Table 8.1) determines how much energy must be produced to ensure that adequate energy is delivered in the time available. (Nielsen, 2012)
Table 8.1 Battlespace Dimensions
| Dimension | Function | Action |
| Latitude | Friendly Force Location | Direction of Weapons
|
| Longitude | Enemy Force Location | Maneuver of Forces |
| Elevation
|
||
| Time | Speed of Maneuver | Timeliness of Attack |
| Timing of Weapon Release | Enemy Vulnerability | |
| Frequency | Bandwidth Required | Rate of Information Flow |
| Bandwidth Available | Interference | |
| Frequency of Transmissions | Vulnerability to Jamming
|
|
| Vulnerability to Intercept
|
Source: (Adamy D. -0., 2015)
THE BELOVED BTU GIVES WAY TO JOULES
Weapons designers favor metric units, where length is in meters, mass in kilograms, and time in seconds. Energy is expressed in Joules. A Joule is approximately the energy required to lift a quart of milk a distance of three feet, or 1/50000 (2 x 10–5) of the energy it takes to brew a cup of coffee. [4] [5]
ENERGY REQUIRED FOR DAMAGE
Damage may be defined as soft damage. For example, attacking a UAS in the air might upset the UAS computers compared to hard damage meaning the complete vaporization of the UAS in the air. The former is sensitive to the details of the attack, the hardness of chips, the computer(s) details, communications, circuits, and sub-circuits. Vaporization produces immediate feedback as to the target status – catastrophic. Two things must be known in determining how much energy a weapon must produce to damage a target. How much energy it takes to damage the target and what fraction of the energy generated will be lost in propagating it. (Nielsen, 2012)
ICE CUBE
Consider the energy required (damage level) to vaporize an ice cube. [6] Pull an ice cube from the refrigerator. If its temperature is below the temperature, it will melt. First, we must raise the temperature to melt temperature. The energy required is proportional to both the necessary ΔT rise and the amount of ice in the cube. From thermodynamics, the expression (specific heat calculation) covering this is: E = m x C (Tm-Ti), where E is the energy required in Joules, m = mass of ice cube in grams, Ti = the initial temperature in Celsius, Tm= melting temperature, C is the heat capacity constant of proportionality (J/gm x o C). For this example, C= 4.2 (J/gm x OC) and ice cube = 50 gm, Ti = -10 (C), Tm= 0 (oC). (Lm) for water = 334 Joules / gm. So, 16,700 additional Joules are necessary to melt the ice cube of 50gm. Tv = vaporization temperature, (100 oC) So, E = 2,100 Joules of energy required to raise it to the melting point. This energy is not enough. We must melt the ice cube. The heat of fusion (Lm) is the energy required to convert 1 gm of solid to 1 gm of liquid. With an additional 16,700 Joules, we now have a small water puddle. But our object is to vaporize the ice cube – hard damage. Using the specific heat equation again, E = m x C (Tv-Tm), we require an additional 21,000 Joules to raise the ice cube as molten water to vapor at the same temperature by supplying the heat of vaporization, Lv = 2,440 Joules per gm of water. This means an additional 122,000 Joules of energy are required. The total energy needed to vaporize an ice cube of 50 gm is 161,000 Joules. Lv accounts for about 75% of the required energy. One little ice cube. In BTUs, this is only 152.7 BTUs.[7] [8]
10,000 JOULES
(Nielsen, 2012) gives a table of thermal properties of Aluminum, Copper, Magnesium, Iron, and Titanium. It shows that most solid materials (See Table 8.2) have a density on the order of 1 – 10 gm /cubic centimeter and that 10,000 Joules is sufficient energy to vaporize about one cubic centimeter of anything! 10,000 Joules is a magic number because it is close to the energy delivered by a wide range of DEWs. (Nielsen, 2012) A typical rifle round has about 10 gm and is fired at a muzzle velocity of 1000 m/s. (Halsam, 1982) This corresponds to kinetic energy (KE) of (mv 2 /2) of 5,000 Joules. A roman Catapult could throw a 20 Kg stone over 200 meters. The KE required for this use is about 40,000 Joules. (Foley, March 1979) A medieval crossbow could launch an 85-gm bolt over 275 meters. This required 13,000 Joules. (Vernard Foley, January 1985)
Table 8.2 Thermal Properties of Common Materials
| Material | Density
Gm/cm3 |
Melting Point, Tm
0C |
Vaporization Point, Tv
0C |
Heat Capacity
(J/gm0C) |
Heat of Fusion
(J/gm) |
Heat of Vaporization
(J/gm) |
| Aluminum | 2.7 | 660 | 2500 | 0.9 | 400 | 1100 |
| Copper | 8.96 | 1100 | 2600 | 0.38 | 210 | 4700 |
| Magnesium | 1.74 | 650 | 1100 | 1.0 | 370 | 5300 |
| Iron | 7.9 | 1500 | 3000 | 0.46 | 250 | 6300 |
| Titanium | 4.5 | 1700 | 3700 | 0.52 | 320 | 8800 |
Source: Table 1-1 (Nielsen, 2012)
ENERGY ALONE SUFFICIENT FOR HARD DAMAGE?
In a nutshell, no. A nuclear bomb releases a lot of energy. One Kiloton yields 4,000,000,000,000
Joules. Well above the 10,000 Joule criterion, but at a distance of less than a mile from detonation, a concrete structure is undamaged. Over the same range, an artillery shell with only 10,000 Joules of energy could easily destroy such a structure. Also, consider the sun. It delivers about 5,000 Joules of energy over every square centimeter of the earth’s surface, yet we see no cars melting or people fried. The energy must be delivered over a small region and in a short time to the target. Energy is not the silver bullet for damage. We must also consider the density of energy on the target (Joules per square centimeter),[9] the rate of energy delivery, or power (Joules/ sec or Watts). The nuclear bomb is not a DE weapon like the artillery shell. Much of the energy released does not intersect with the concrete structure and is “wasted .”The artillery shell is a DE and concentrates its energy on the target in question. Suppose we spread the bomb’s energy over a sphere’s surface at a range of one mile. In that case, the energy density is only 13 Joules per square centimeter, far less than the DE artillery shell density of 10,000 Joules per square centimeter. The nuclear bomb is consistent with other weapon types, with the Spreading of blast energy accounted for. (Nielsen, 2012)[10] See Figure 8.1.
Figure 8.1 Energy Deposition from Bombs and DEW
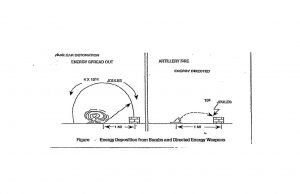
Source: Adapted from Figure 1-2 in (Nielsen, 2012)
ENERGY DELIVERY RATE
If energy is delivered over too long a period, it is not effective in damaging the intended target. The target can shed energy as rapidly as it is deposited. Cars in a parking lot heat up in the sun (unfortunately fatal to youngsters or animals left in the car) until they become so hot that they radiate energy away as rapidly as it’s deposited, so they don’t heat up to the point of sustained damage. After that, they heat up to a constant temperature. If energy is delivered more rapidly than the target can handle, the damage will ensue. (Nielsen, 2012)
From thermodynamics, we know that energy can be transferred away (lost in propagation) from a target by thermal conduction, convection, and radiation.
THERMAL CONDUCTION
Thermal conduction losses (energy flow or “downhill” temperature gradient (slope of the curve of temperature v distance) from hot regions to cold regions, moving the temperature to equilibrium in the system). The steeper the slope, the faster the energy will flow. The equation for thermal conduction is
U = -k( dT / dx) Equation 8.1
Where U = rate of flow of energy across a surface, J/cm2 sec
dT / dx = the slope (derivative of Temperature / distance) of the temperature curve,
degrees / cm
k = constant of proportionality called thermal conductivity[11] in J/ sec cm deg
.
The thermal conductivity can vary greatly from one material to another. As a result of the energy flow U, the temperature T in different target regions will change. See Figure 8.2.
Figure 8.2 Energy Flow and Resulting Change in Temperature
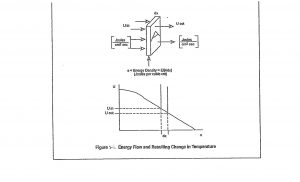
Source: Adapted from Figure 1-4 (Nielsen, 2012)
Energy flows until the temperature is the same everywhere in the system, called equilibrium. Figure 8.2 shows how knowing U throughout a target can calculate the rate of temperature change within it. (Nielsen, 2012) Figure 8.2 shows a thin region within the target having cross-section A and a thickness of dx. There is a flow of energy (Joules /square centimeter per second) into the region, Uin, and flow out of the region, denoted Uout. If these two quantities are not equal, then the amount of energy within the region will increase or decrease ( will change), and the temperature will rise or fall ( it will also change). In Figure 8.2, the flow out is less than the flow in, which means the temperature will increase. The rate of change in temperature is found using the thermal diffusion equation 8.2 (Nielsen, 2012)
dT / dt = (k/Cρ) (d2T / dx2) Equation 8.2
where: (Uin – Uout) is the energy flow into and out of the region
dT / dx is the change in temperature gradient across the region
C the heat capacity
k = thermal conductivity
ρ = density of target material (gm/cm3)
k/Cρ = thermal diffusivity = D[12]
CONSTANT SURFACE TEMPERATURE CASE
Although the diffusion equation is second order and usually requires a computer to assist in solutions, there is one special case of interest in studying DEW effects. Figure 8.3 shows how the temperature on the interior of a solid varies with time if the surface is maintained at a constant temperature. (Nielsen, 2012)
Figure 8.3 Special Case: Constant Surface Temperature
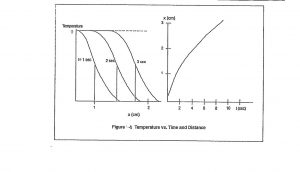
Source: Adapted from Figure 1-5 (Nielsen, 2012)
The heated region propagates into the target on the left side of the figure, eventually being heated to a temperature of T. The distance to the target to which the heat is propagated is plotted as a function of time on the right side. The distance obeys a simple law:
x ~ √Dt Equation 8.3
k/Cρ = thermal diffusivity = D
t = time
x = distance
C the heat capacity
k = thermal conductivity
ρ = density of target material (gm/cm3)
The distance to the target is approximately equal to the square root of the Diffusivity times the elapsed time. This equation is used in developing criteria for target damage from different weapon concepts (laser, microwave, and particle beams). (Nielsen, 2012)
CONVECTION
Thermal conduction arises because of the random motion of molecules. Hot molecules give up energy by motion; cold molecules warm up by gaining energy. The movement of both types of molecules is always towards equilibrium T.
Convection (heat loss by the macroscopic motion of molecules). Think of an attic fan moving hot air out of the attic, where the fan blades induce motion. The macroscopic flow of air induced by the fan can carry away hot air from the attic and lower the temperature more efficiently than conduction. Convection is an important source of energy loss. Many targets, such as airplanes, drones, boats, or UUVs, can move rapidly through the air. (See Figure 8.4) The wind of motion (think sailboat or airplane) across the surface of the target is an important factor in establishing the damage threshold. Weapons like lasers deposit energy primarily on the surface of the target. Hot air rises and is lighter than cold air. The process of heating a region itself can set air into motion, affecting the threshold and extent of the damage. (Nielsen, 2012)
The expression for wind induced convection for temperature v distance:
dT / dt = – V dT/ dx Equation 8.4
Where V = wind velocity
T = temperature in time at point x
dT /dx is the rate of change of temperature in time at point x
Figure 8.4 Effect of Wind v Temperature

Source: Adapted from Figure 1-6 (Nielsen, 2012)
WIND vs. TEMPERATURE CONVECTION HEAT
Figure 8.4 shows how convection heat is handled. dT / dx is a region of space in which the temperature gradient varies with distance. Wind of velocity V and time dt blows the temperature profile downstream to the point indicated by the dotted line. The temperature at point x drops in time dt from T to T-V (dT /dx) dt. The gradient or rate of change of T in time at point x is dT /dt = – V dT /dx. This expression for the effect of wind on the temperature at a point is clever. If the wind velocity V is stronger, the temperature drops more rapidly, and if the temperature is the same everywhere, the gradient dT /dx is zero. The wind serves only to replace hot air with more hot air temperature stays the same. (Nielsen, 2012)
VACUUM BLACK BODY RADIATION
To lose energy by conduction or convection, a target must be immersed in the atmosphere, water, or some fluid medium to supply the necessary molecules to carry the energy away. (Adamy D. L., 2004) Targets in a vacuum of outer space can lose energy through radiation.
Molecule movement is not just random; they vibrate, rotate, and incorporate energy in their internal structure. The energy that temperature represents resides in internal degrees of freedom. Molecules can give up internal energy by emitting electromagnetic radiation such as light, radio waves, and microwaves.
Black Body radiation can occur in space or a vacuum. Black Body radiation is an ideal mathematical surface that absorbs all radiation incident. In equilibrium, it would radiate more energy than any other object. (Nielsen, 2012)
The total Intensity of radiation emerging from the surface of a Black Body, S (Watts/cm2), is:
S = σ T4 Equation 8.5
Where σ = Stefan-Boltzmann constant = 5.67 x 10-12 (Watts/cm2 K4),
K= Kelvin temperature.
S = radiation emerging from the surface of a Black Body (Watts/cm2)
Figure 8.5 shows the strong dependence of Black Body radiation on temperature. Radiation loss is not important until higher temperatures are reached. Black Body radiation is the upper bound and represents the perfect case.
Figure 8.5 Black Body Radiation
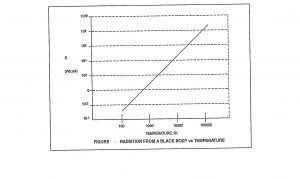
Source: Adapted from Figure 1-7 (Nielsen, 2012)
IMPLICATIONS
Damaging targets depend not only on delivering energy but also on concentrating the energy in both space and time. In space, we deliver about 10,000 Joules per cm2 of the target surface, either at a single point (bullet) or over the whole surface, as in a nuclear weapon. In time, energy must be delivered more rapidly than the target can shed energy through conduction, convection, and radiation loss mechanisms. The fluence (Joules / cm2) or Intensity (Watts /cm2) necessary to damage a target will vary with the time or pulse width that the weapon engages the target. (Nielsen, 2012)
The goal is to look at how a DEW deposits energy in a target and then consider energy deposition and loss rates to determine the criteria for damaging the target.
FLUENCE AND INTENSITY
Two concepts are used frequently in determining criteria for target damage assessments. Fluence is the energy per area (Joules / cm2) necessary to damage a target. Intensity is the power per area (Watt / cm2) necessary to damage a target. Both vary with time or pulse width that the weapon engages the target and have the form shown in Figure 8.6. For extremely short times, energy is deposited into the target so rapidly that there is no way for radiation, conduction, or other energy loss mechanisms to carry it away. For short pulse widths less than t1, the fluence necessary to damage the target is constant, and the Intensity necessary to damage it decreases linearly. At longer interaction times, t1 and t2, some of the energy deposited is carried away before contributing to the damage. The fluence in this case to achieve damage begins to rise with pulse width. Beyond the long width t2, energy is deposited too slowly to damage unless some minimum intensity is exceeded, and the energy threshold is proportional to the pulse width. (Nielsen, 2012)
Figure 8.6 Fluence and Intensity
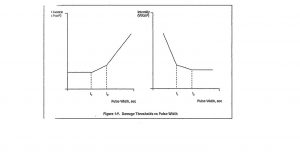
Source: Adapted from Figure 1-8 (Nielsen, 2012)
ALL-PURPOSE DAMAGE CRITERIA
10,000 Joules is a reasonable first approximation damage criteria in developing weapon parameters that are likely to achieve damage. This is certainly true for hard damage mechanisms like melting or vaporization. We are talking about delivering a fluence (104 J/cm2 ) which for most weapons will damage targets on time scales too short for the energy to be rejected. (Nielsen, 2012) This was evidenced in Table 8.2. Figure 8.7 suggests the reason for this magic number. It shows the depth to which 104 Joules vaporizes a target as a function of the area over which the energy is spread. 104 Joules can only vaporize a significant depth of target when over which it is spread has a fluence on the order of 104 J/cm2. At significantly lower fluences, the depth vaporized would not be sufficient even to penetrate the skin of most targets. (Nielsen, 2012) Nielsen suggests that 104 Joules / cm2 is the magic criterion because so many weapons place energies on the order of 104 J /cm2. Making a hole in a target to the depth of 1 centimeter is sufficient to damage almost anything. Many targets are less than 1 cm thick if we count the thickness of the solid matter that must be penetrated to prevent the target from functioning. The outer surface of a car is sheet metal less than 1 centimeter. If a weapon (104 J / cm2) were to propagate through the air and penetrate the surface near the gas tank, the car might blow up or catch fire. The same weapon would not affect the engine block. (Nielsen, 2012)
Figure 8.7 Depth Vaporized by 104 Joules v Area Engaged and Fluence.
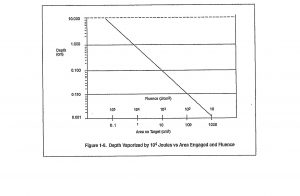
Source: Adapted from Figure 1-9 (Nielsen, 2012)
ENERGY SPREAD AND LOSS IN PROPAGATION
There are two types of energy losses in propagation: the Spreading of energy such that it does not interact with the target and the wasting of energy in interactions with a physical medium, such as the atmosphere, through which it passes to destroy the target. Type one occurs whether the weapon or target is located on earth or in the vacuum of space. Type two occurs primarily when a weapon or target lies within the atmosphere. Table 8.3 shows the Energy losses in propagation as a function of weapon type and loss mechanisms.
Table 8.3 Energy losses in propagation
| Weapon Type | Energy Loss Mechanism |
| Kinetic Energy (bullets, rockets) | Atmospheric Drag |
| Lasers | Absorption by molecules |
| Scattering by molecules | |
| Absorption by aerosols (small particles) | |
| Scattering by aerosols | |
| Microwaves | Absorption by molecules |
| Scattering by molecules | |
| Absorption by water droplets | |
| Scattering by water droplets | |
| Particle Beams | Energy losses to electrons |
| Scattering from nuclei | |
| Scattering from electrons | |
| Radiation |
Source: (Nielsen, 2012)
ENERGY SPREAD
There are opposite ends of weapon types to consider in discussing damage criteria. DEW, in which all the energy transmitted is brought to bear on the target, and bombs in which the energy is spread out indiscriminately over an ever-expanding space. Real weapons fall in between these extremes. (Nielsen, 2012) Every weapon has an inherent “spread” of energy associated with its propagation. The terms divergence and jitter describe the two types of spread usually observed. The former has to do with natural phenomena like the diffraction of light from a laser. The latter term, for instance, has to do with the lack of repeatability of the shot group with bullets fired by a skilled shooter at a target at a range z. See Figure 8-8 for clarity of energy spread. Both Divergence and jitter are measures of departure from perfect energy propagation aimed at a target. (Nielsen, 2012)
Figure 8.8 Divergence and Jitter
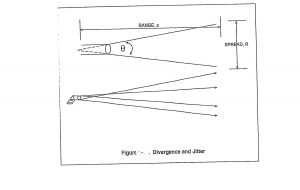
Source: Adapted from Figure 1-11 (Nielsen, 2012)
CONCLUSIONS
In essence, the study of DEW is a study of energy – how it propagates to, interacts with, and is redistributed within a target. The goal of using a DEW – especially aimed at CBRN from the air via drones – is to determine under what conditions sufficient energy will accumulate within a target to damage it. To achieve damage, energy must be concentrated both in space and time. (Nielsen, 2012) Fundamentally we have:
- The necessary fluence for a hard target kill is on the order of 10,000 J / square cm. [13]
- For 10,000 Joules / square cm to achieve damage, it must be concentrated in time so that it cannot flow and be redistributed within the target.
- The loss and redistribution of energy occur through conduction, convection, and radiation. Either fluence or Intensity becomes a limiting threshold when these heat loss mechanisms are in play.
- DEW ideally propagates energy directly at a target. Real-life spreads energy through Divergence and jitter.
- In the atmosphere, various loss mechanisms ( absorption, scatter, etc.) cause a fraction of the energy directed at a target to be lost in the propagation to it,
- DEW must be capable of giving up energy over the range of propagation to the target and still place sufficient fluence or Intensity on the target to damage it. (Nielsen, 2012)
- UAS /Drones and UUV are capable of deploying/delivering energy to a target – especially CBRN assets because of their high value and impact on human life. (Nichols R. K., Hardening US Unmanned Systems Against Enemy Counter Measures, 2019)
Bibliography
Adamy, D. -0. (2015). EW 104 EW Against a New Generation of Threats. Boston: Artech House.
Adamy, D. (2001). EW 101 A First Course in Electronic Warfare. Boston, MA: Artech House.
Adamy, D. (2009). EW 103 Tactical Battlefield Communications Electronic Warfare. Boston, MA: Artech House.
Adamy, D. L. (2004). EW 102 A Second Course in Electronic Warfare. Boston: Artech House.
Beason, D. (2005). The E-Bomb: How America’s new directed energy weapons will change the way future wars will be fought. Cambridge, MA: Da Capo Press.
Foley, W. S. (March 1979). Ancient Catapults. Scientific American, 240, 150.
Glasstone, S. &. (1977). The Effects of Nuclear Weapons, 3rd Edition. In S. &. Glasstone, Chapter V, Figures 5.20, 5.22 & 5.23. Washington, DC: UGPO.
Halsam, C. M.-S. (1982). Small Arms and Cannons. Oxford: Brassey’s Publishers.
Nichols, R. K. (2019, March 14). Hardening US Unmanned Systems Against Enemy Counter Measures. 7th Annual Unmanned Systems Summit. Alexandria, VA, USA: PPTX presentation, self.
Nichols, R. K., & Sincavage, S. M. (2021). Disruptive Technologies with Applications in Airline, Marine, and Defense Industries. Manhattan, KS: New Prairie Press #38.
Nichols, R. K., Mumm, H. C., Lonstein, W. D., Ryan, J. J., Carter, C., & and Hood, J.-P. (2019). Unmanned Aircraft Systems in the Cyber Domain, 2nd Edition. Manhattan, KS: NPP eBooks. 27. Retrieved from www.newprairiepress.org/ebooks/27
Nielsen, P. E. (2012). Effects of Directed Energy Weapons. Middletown, DE: CreateSpace Independent Publishing Platform.
Vernard Foley, G. P. (January 1985). The Crossbow. Scientific American, 252, 104.
ENDNOTES
[1] Nielson’s book is an inspiration for a few chapters in our book. (Nielsen, 2012) has been chosen by the Director of the UAS Cybersecurity graduate program as a textbook. We are indebted to Phillip E. Nielsen for his work.
[2] Philip E. Nielsen is a director and senior technical advisor for MacAulay-Brown, Incorporated, a defense engineering services firm headquartered in Dayton, Ohio. Before joining MacAulay-Brown, Dr. Nielsen served on active duty with the U.S. Air Force (USAF) for 26 years, retiring as a colonel. During this period, he served in various positions related to the research, development, and acquisition of advanced weapon systems. He received the USAF Research and Development Award for his contribution to high-energy laser physics in 1975. Phillip E Nielsen was associated with the National Defense University (1987-1988) and The USAF Studies and Analyses Agency. Dr. Nielsen has produced a brilliant discussion of DEW. The authors of this book give full attribution to Dr. Nielsen for his contributions.
[3] Nuclear weapons may be characterized by megatons, bullets in terms of muzzle velocity, and particle beams in terms of amperes of current. The commonality is the amount of energy absorbed by the target, which leads to similar levels of damage achieved at similar levels of energy deposited. (Nielsen, 2012)
[4] No self-respecting American chemical engineer would think in terms of metrics or Joules. English units are preferred (remember the ’60-’70s gas pump fiascos in liters?) So, 1 m = 3 ft., 1 BTU = 1,054.35 J, 1lb = 0.454 kg. However, the literature calls for Joules – so be it. Protest noted.
[5] See (Nielsen 2012) Appendix A for standard units used in this chapter or any modern physics reference.
[6] For us old-time American engineers for reference points: 1 BTU = 1055 J; 1 Calorie = 4.19 J; 1kw hr = 3.6 x 106 J; 1eV = 1.6 x 10-19 J and 1 erg = 10-7 J.
[7] Hmm, maybe weapons designers have inflated egos. Joules sound more impressive. One ice cube. This is a standard type of chemical engineering problem. The ice cube is raised enough to make it a puddle of water (soft design). The object is to vaporize the target completely. This means we have to keep adding energy to change states, raise the ice +water to water to water plus steam, and finally to only steam. The total energy balance is 2,100 + 16,700 + 21,000 + 122,000 = 161,800 Joules. The Latent heat of vaporization accounts for ~ 75% of the destruction. A lot of energy goes into separating the bonds and structure of the molecules to disperse them into vapor. A plot of Temperature v energy deposited in Watts (Watts = Joules/sec) demonstrates that the majority and time and energy are taken up vaporizing the molten cube (hard design).
[8] A standard ton of air conditioning removes 12,000 BTUs/ hr (3.5 kW). Industrial towers remove 15,000 BTUs /hr = 1 ton to account for inefficiency in the compressor. As a comparison, a rule of thumb is ~ 420 kJ / Kg (970 BTU/LB) of heat energy absorbed for evaporated water in an open circuit cooling tower.
[9] Aka called “Fluence” Units of fluence are 1 J/cm2 =104 J/m2 and 1 W /cm2 = 104 W/ m2
[10] The effect of the area can be better understood by looking at the energy delivery from the two atom bombs delivered against Hiroshima and Nagasaki. (Glasstone, 1977) Both weapons had yields of about 20kT; they released about 8 x 1013 Joules of energy. At a range of z of 0.1 mile (= 1.6 x 104 cm), the energy density would be approximately 8 x 1013 Joules / 4πz2 = 2.5 x 104 J /cm2 or fluence. So, when the Spreading of the blast energy is accounted for, the result is consistent with other weapon types. Our damage energy density sufficiency is 10,000 J / cm2 or fluence.
[11] Thermal conductivity varies for materials. Copper (good conductor) = 4.2 J/cm sec deg whereas air (thermal insulator) has a value of 0.00042 J /cm sec deg. (Nielsen, 2012) Thermal conductivity is not just a simple single-order equation. Other effects are observed changes in regional temperatures, thermal conductivity, diffusion/diffusivity, and temperature propagation v time
[12] Thermal diffusivity does not vary much from one material to another.
[13] This serves as the upper bound since many targets of interest will be damaged at lower fluences.

