Appendix A dB MATH AND PLANE / SPHERICAL TRIGONOMETRY PRIMER

DECIBEL MATH

EW calculations are done using “dB” math. It allows manipulation of very large numbers such as transmitted signal strength and very small numbers such as received signal strength. Numbers expressed in decibels (or dB) form are logarithmic and follow the rules.[1] This permits the comparison of values that may differ in many orders of magnitude. It is important to understand that any value expressed in decibel units is a ratio converted to a logarithmic form. (Adamy D. , EW 101: A First Course in Electronic Warfare, 2001)

To Convert To Decibel Form (base 10 log)

Ratio (in dB) = 10 log (Linear Ratio)                                                                         Eq. A-1

Example:  convert 2 (the ratio of 2 to 1) to decibel form.

10 log (2)  = 3 dB  (rounded)

convert 1/2 (the ratio of 1 to 2) to decibel form.

10 log (0.5) = – 3 dB   in EW, link loss and antenna calculations this is a useful factor.

A reverse way of looking at the process or converting back to a nonlogarithmic form is:

Antilog (logarithm number)  = linear number in place of 10 (logarithmic number)     Eq. A-2

So, antilog (3/10) = 2. See (Adamy D. , EW 101: A First Course in Electronic Warfare, 2001) or (Adamy D. L., 2004) or (Adamy D. L., Space Electronic Warfare, 2021) for many examples of nauseating details and helpful tables for common usage.

PLANE TRIG / EQUATIONS

To solve problems of elevation and azimuth of look angles associated with Earth Satellites, three-dimensional (3-D) angular relationships are solved with Plane and Spherical Trigonometry.  Plane Trigonometry deals with triangles in a plane.  The important relationships are:

Plane Trigonometry:

The Law of Sines: ;                                                                                    Eq. A-3

Note: Lower case letters represent the lengths of a triangle’s side, and upper-case letters are their associated angles opposite the corresponding side.

The Law of Cosines for Sides: a2 = b2 + c2 – 2bc cos A                         Eq.  A-4

The Law of Cosines for Angles: A = b cos C + c cos B                           Eq.  A-5

A right triangle is a plane triangle with a 90° angle.  All triangles fall under the above rules.

Right Triangle: 2-dimensional defined, also known as a Plane Triangle.

Figure  A-1:  Right Triangle

 Source: Courtesy of: (Adamy D. L., Space Electronic Warfare, 2021)

Spherical Trigonometry:

The Law of Sines for Spherical Triangle:                          Eq. A-6

The Law of Cosines for Sides: cos a = cos B cos C + sin B sin C cos a                 Eq. A-7

The Law of Cosines for Angles: cos A = -cos B cos C + sin B sin C cos a            Eq. A-8

Spherical Triangle: Formed by 3 great circles that pass through a common center point.

Figure  A-2: Triangle on a Sphere

 Source: Courtesy of:  (Adamy D. L., Space Electronic Warfare, 2021)

Napier’s Rules:

Right spherical triangles allow the use of simplified spherical trigonometric equations using Napier’s rules.

Figure A-3: Napier’s Rules for Right Spherical Triangles

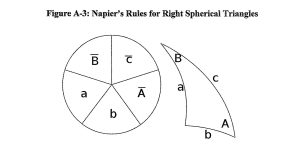
Source: Author modification of Figure 2.6, Courtesy of:  (Adamy D. L., Space Electronic Warfare, 2021)

Rules for Napier’s right spherical triangles

sin a = tan b cotan B;                  Eq.  A-9

cos A = cotan c tan b;                 Eq.  A-10

cos c = cos a cos b;                      Eq.  A-11

sin a = sin A sin c                         Eq.  A-12