Main Body
Chapter 5. Monopolistic Competition and Oligopoly
5.1 Market Structures
5.1.1 Market Structure Spectrum and Characteristics
Table 5.1 shows the four major categories of market structures and their characteristics.
Table 5.1 Market Structure Characteristics
|
Perfect Competition |
Monopolistic Competition |
Oligopoly |
Monopoly |
|
|
|
|
|
|
Homogeneous good |
Differentiated good |
Differentiated good |
One good |
|
Numerous firms |
Many firms |
Few firms |
One firm |
|
Free entry and exit |
Free entry and exit |
Barriers to entry |
No entry |
Perfect competition is on one end of the market structure spectrum, with numerous firms. The word, “numerous” has special meaning in this context. In a perfectly competitive industry, each firm is so small relative to the market that it cannot affect the price of the good. Each perfectly competitive firm is a price taker. Therefore, numerous firms means that each firm is so small that it is a price taker.
Monopoly is the other extreme of the market structure spectrum, with a single firm. Monopolies have monopoly power, or the ability to change the price of the good. Monopoly power is also called market power, and is measured by the Lerner Index.
This chapter defines and describes two intermediary market structures: monopolistic competition and oligopoly.
Monopolistic Competition = A market structure characterized by a differentiated product and freedom of entry and exit.
Monopolistically Competitive firms have one characteristic that is like a monopoly (a differentiated product provides market power), and one characteristic that is like a competitive firm (freedom of entry and exit). This form of market structure is common in market-based economies, and a trip to the grocery store reveals large numbers of differentiated products: toothpaste, laundry soap, breakfast cereal, and so on.
Next, we define the market structure oligopoly.
Oligopoly = A market structure characterized by barriers to entry and a few firms.
Oligopoly is a fascinating market structure due to interaction and interdependency between oligopolistic firms. What one firm does affects the other firms in the oligopoly.
Since monopolistic competition and oligopoly are intermediary market structures, the next section will review the properties and characteristics of perfect competition and monopoly. These characteristics will provide the defining characteristics of monopolistic competition and oligopoly.
5.1.2 Review of Perfect Competition
The perfectly competitive industry has four characteristics:
(1) Homogenous product,
(2) Large number of buyers and sellers (numerous firms),
(3) Freedom of entry and exit, and
(4) Perfect information.
The possibility of entry and exit of firms occurs in the long run, since the number of firms is fixed in the short run.
An equilibrium is defined as a point where there is no tendency to change. The concept of equilibrium can be extended to include the short run and long run.
Short Run Equilibrium = A point from which there is no tendency to change (a steady state), and a fixed number of firms.
Long Run Equilibrium = A point from which there is no tendency to change (a steady state), and entry and exit of firms.
In the short run, the number of firms is fixed, whereas in the long run, entry and exit of firms is possible, based on profit conditions. We will compare the short and long run for a competitive firm in Figure 5.1. The two panels in Figure 5.1 are for the firm (left) and industry (right), with vastly different units. This is emphasized by using “q” for the firm’s output level, and “Q” for the industry output level. The graph shows both short run and long run equilibria for a perfectly competitive firm and industry. In short run equilibrium, the firms faces a high price (PSR), produces quantity QSR at PSR = MC, and earns positive profits πSR.
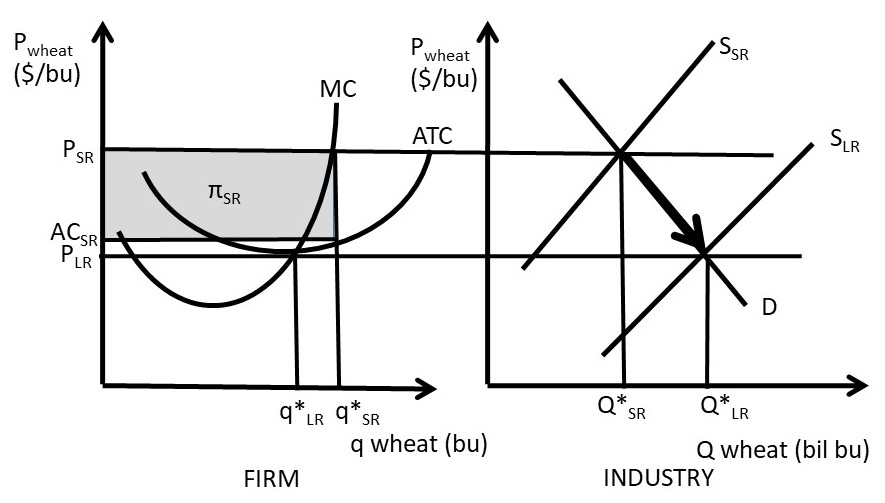
Figure 5.1 Short Run and Long Run Equilibria for a Perfectly Competitive Firm
Positive profits in the short run (πSR > 0) lead to entry of other firms, as there are no barriers to entry in a competitive industry. The entry of new firms shifts the supply curve in the industry graph from supply SSR to supply SLR. Entry will occur until profits are driven to zero, and long run equilibrium is reached at Q*LR. In the long run, economic profits are equal to zero, so there is no incentive for entry or exit. Each firm is earning exactly what it is worth, the opportunity costs of all resources. In long run equilibrium, profits are zero (πLR = 0), and price equals the minimum average cost point (P = min AC = MC). Marginal costs equal average costs at the minimum average cost point. At the long run price, supply equals demand at price PLR.
5.1.3 Review of Monopoly
The characteristics of monopoly include: (1) one firm, (2) one product, and (3) no entry (Table 5.1). The monopoly solution is shown in Figure 5.2.
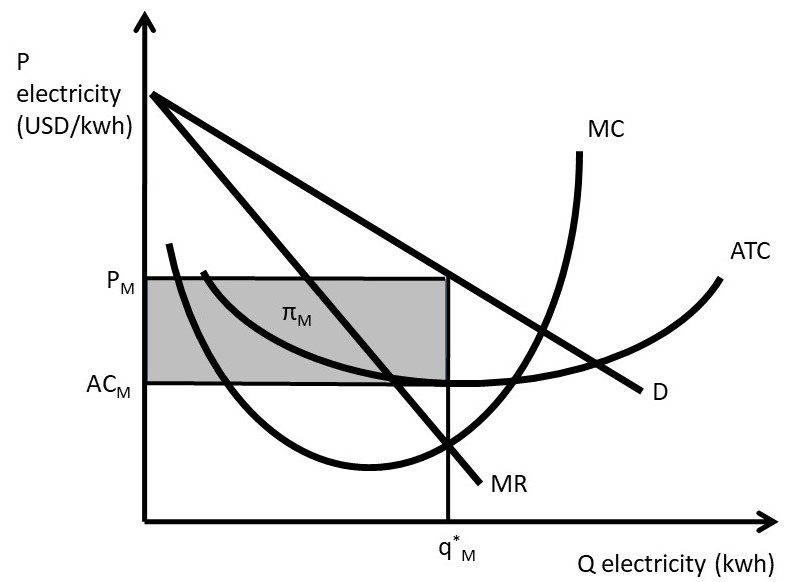
Figure 5.2 Monopoly Profit Maximization
Note that long-run profits can exist for a monopoly, since barriers to entry halt any potential entrants from joining the industry. In the next section, we will explore market structures that lie between the two extremes of perfect competition and monopoly.
5.2 Monopolistic Competition
Monopolistic competition is a market structure defined by free entry and exit, like competition, and differentiated products, like monopoly. Differentiated products provide each firm with some market power. Advertising and marketing of each individual product provide uniqueness that causes the demand curve of each good to be downward sloping. Free entry indicates that each firm competes with other firms and profits are equal to zero on long run equilibrium. If a monopolistically competitive firm is earning positive economic profits, entry will occur until economic profits are equal to zero.
5.2.1 Monopolistic Competition in the Short and Long Runs
The demand curve of a monopolistically competitive firm is downward sloping, indicating that the firm has a degree of market power. Market power derives from product differentiation, since each firm produces a different product. Each good has many close substitutes, so market power is limited: if the price is increased too much, consumers will shift to competitors’ products.
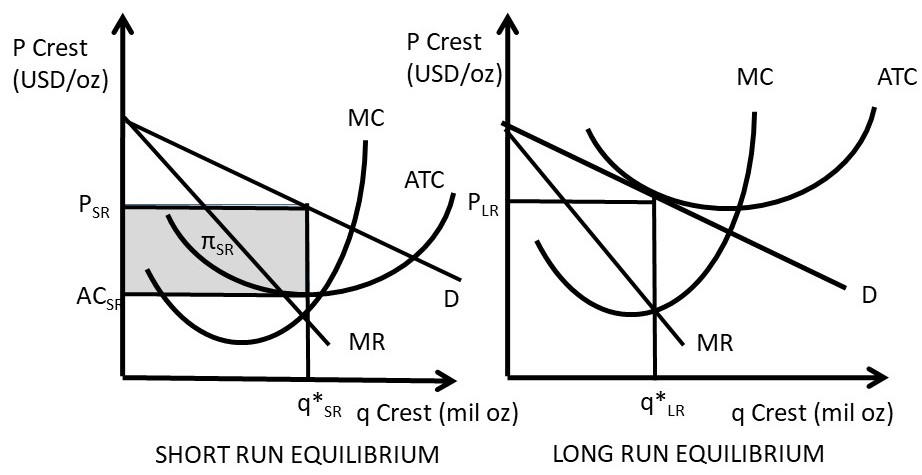
Figure 5.3 Monopolistic Competition in the Short Run and Long Run
Short and long run equilibria for the monopolistically competitive firm are shown in Figure 5.3. The demand curve facing the firm is downward sloping, but relatively elastic due to the availability of close substitutes. The short run equilibrium appears in the left hand panel, and is nearly identical to the monopoly graph. The only difference is that for a monopolistically competitive firm, the demand is relatively elastic, or flat. Otherwise, the short run profit-maximizing solution is the same as a monopoly. The firm sets marginal revenue equal to marginal cost, produces output level q*SR and charges price PSR. The profit level is shown by the shaded rectangle π.
The long run equilibrium is shown in the right hand panel. Entry of other firms occurs until profits are equal to zero; total revenues are equal to total costs. Thus, the demand curve is tangent to the average cost curve at the optimal long run quantity, q*LR. The long run profit-maximizing quantity is found where marginal revenue equals marginal cost, which also occurs at q*LR.
5.2.2 Economic Efficiency and Monopolistic Competition
There are two sources of inefficiency in monopolistic competition. First, dead weight loss (DWL) due to monopoly power: price is higher than marginal cost (P > MC). Second, excess capacity: the equilibrium quantity is smaller than the lowest cost quantity at the minimum point on the average cost curve (q*LR < qminAC). These two sources of inefficiency can be seen in Figure 5.4.
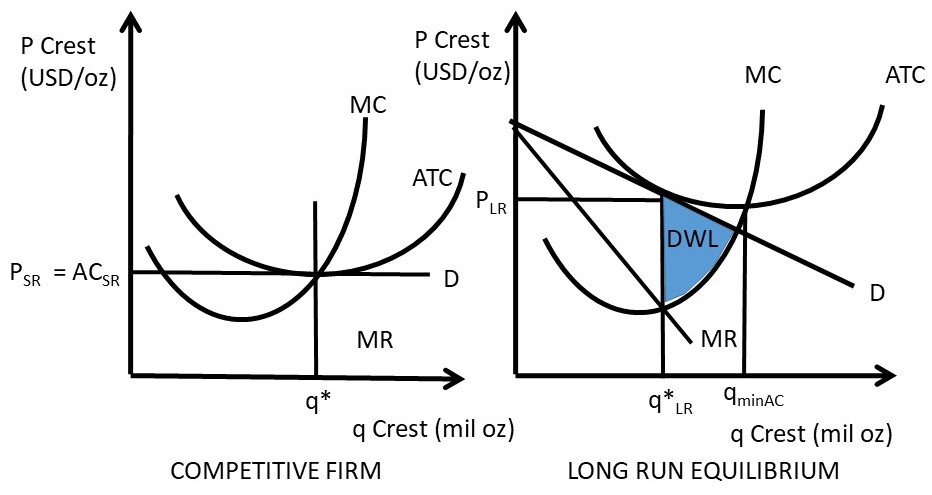
Figure 5.4 Comparison of Efficiency for Competition and Monopolistic Competition
First, there is dead weight loss (DWL) due to market power: the price is higher than marginal cost in long run equilibrium. In the right hand panel of Figure 5.4, the price at the long run equilibrium quantity is PLR, and marginal cost is lower: PLR > MC. This causes dead weight loss to society, since the competitive equilibrium would be at a larger quantity where P = MC. Total dead weight loss is the shaded area beneath the demand curve and above the MC curve in figure 5.4.
The second source of inefficiency associated with monopolistic competition is excess capacity. This can also be seen in the right hand panel of Figure 5.4, where the long run equilibrium quantity is lower than the quantity where average costs are lowest (qminAC). Therefore, the firm could produce at a lower cost by increasing output to the level where average costs are minimized.
Given these two inefficiencies associated with monopolistic competition, some individuals and groups have called for government intervention. Regulation could be used to reduce or eliminate the inefficiencies by removing product differentiation. This would result in a single product instead of a large number of close substitutes.
Regulation is probably not a good solution to the inefficiencies of monopolistic competition, for two reasons. First, the market power of a typical firm in most monopolistically competitive industries is small. Each monopolistically competitive industry has many firms that produce sufficiently substitutable products to provide enough competition to result in relatively low levels of market power. If the firms have small levels of market power, then the deadweight loss and excess capacity inefficiencies are likely to be small.
Second, the benefit provided by monopolistic competition is product diversity. The gain from product diversity can be large, as consumers are willing to pay for different characteristics and qualities. Therefore, the gain from product diversity is likely to outweigh the costs of inefficiency. Evidence for this claim can be seen in market-based economies, where there is a huge amount of product diversity.
The next chapter will introduce and discuss oligopoly: strategic interactions between firms!
5.3 Oligopoly Models
An oligopoly is defined as a market structure with few firms and barriers to entry.
Oligopoly = A market structure with few firms and barriers to entry.
There is often a high level of competition between firms, as each firm makes decisions on prices, quantities, and advertising to maximize profits. Since there are a small number of firms in an oligopoly, each firm’s profit level depends not only on the firm’s own decisions, but also on the decisions of the other firms in the oligopolistic industry.
5.3.1 Strategic Interactions
Each firm must consider both: (1) other firms’ reactions to a firm’s own decisions, and (2) the own firm’s reactions to the other firms’ decisions. Thus, there is a continuous interplay between decisions and reactions to those decisions by all firms in the industry. Each oligopolist must take into account these strategic interactions when making decisions. Since all firms in an oligopoly have outcomes that depend on the other firms, these strategic interactions are the foundation of the study and understanding of oligopoly.
For example, each automobile firm’s market share depends on the prices and quantities of all of the other firms in the industry. If Ford lowers prices relative to other car manufacturers, it will increase its market share at the expense of the other automobile companies.
When making decisions that consider the possible reactions of other firms, firm managers usually assume that the managers of competing firms are rational and intelligent. These strategic interactions form the study of game theory, the topic of Chapter 6 below. John Nash (1928-2015), an American mathematician, was a pioneer in game theory. Economists and mathematicians use the concept of a Nash Equilibrium (NE) to describe a common outcome in game theory that is frequently used in the study of oligopoly.
Nash Equilibrium = An outcome where there is no tendency to change based on each individual choosing a strategy given the strategy of rivals.
In the study of oligopoly, the Nash Equilibrium assumes that each firm makes rational profit-maximizing decisions while holding the behavior of rival firms constant. This assumption is made to simplify oligopoly models, given the potential for enormous complexity of strategic interactions between firms. As an aside, this assumption is one of the interesting themes of the motion picture, “A Beautiful Mind,” starring Russell Crowe as John Nash. The concept of Nash Equilibrium is also the foundation of the models of oligopoly presented in the next three sections: the Cournot, Bertrand, and Stackelberg models of oligopoly.
5.3.2 Cournot Model
Augustin Cournot (1801-1877), a French mathematician, developed the first model of oligopoly explored here. The Cournot model is a model of oligopoly in which firms produce a homogeneous good, assuming that the competitor’s output is fixed when deciding how much to produce.
A numerical example of the Cournot model follows, where it is assumed that there are two identical firms (a duopoly), with output given by Qi (i=1,2). Therefore, total industry output is equal to: Q = Q1 + Q2. Market demand is a function of price and given by Qd = Qd(P), thus the inverse demand function is P = P(Qd). Note that the price depends on the market output Q, which is the sum of both individual firm’s outputs. In this way, each firm’s output has an influence on the price and profits of both firms. This is the basis for strategic interaction in the Cournot model: if one firm increases output, it lowers the price facing both firms. The inverse demand function and cost function are given in Equation 5.1.
(5.1) P = 40 – QC(Qi) = 7Qi i = 1,2
Each firm chooses the optimal, profit-maximizing output level given the other firm’s output. This will result in a Nash Equilibrium, since each firm is holding the behavior of the rival constant. Firm One maximizes profits as follows.
max π1 = TR1 – TC1
max π1 = P(Q)Q1 – C(Q1)[price depends on total output Q = Q1 + Q2]
max π1 = [40 – Q]Q1 – 7Q1
max π1 = [40 – Q1 – Q2]Q1 – 7Q1
max π1 = 40Q1 – Q12 – Q2Q1 – 7Q1
∂π1/∂Q1= 40 – 2Q1 – Q2 – 7 = 0
2Q1 = 33 – Q2
Q1* = 16.5 – 0.5Q2
This equation is called the “Reaction Function” of Firm One. This is as far as the mathematical solution can be simplified, and represents the Cournot solution for Firm One. It is a reaction function since it describes Firm One’s reaction given the output level of Firm Two. This equation represents the strategic interactions between the two firms, as changes in Firm Two’s output level will result in changes in Firm One’s response. Firm One’s optimal output level depends on Firm Two’s behavior and decision making. Oligopolists are interconnected in both behavior and outcomes.
The two firms are assumed to be identical in this duopoly. Therefore, Firm Two’s reaction function will be symmetrical to the Firm One’s reaction function (check this by setting up and solving the profit-maximization equation for Firm Two):
Q2* = 16.5 – 0.5Q1
The two reaction functions can be used to solve for the Cournot-Nash Equilibrium. There are two equations and two unknowns (Q1 and Q2), so a numerical solution is found through substitution of one equation into the other.
Q1* = 16.5 – 0.5(16.5 – 0.5Q1)
Q1* = 16.5 – 8.25 + 0.25Q1
Q1* = 8.25 + 0.25Q1
0.75Q1* = 8.25
Q1* = 11
Due to symmetry from the assumption of identical firms:
Qi = 11 i = 1,2Q = 22units P = 18 USD/unit
Profits for each firm are:
πi = P(Q)Qi – C(Qi) = 18(11) – 7(11) = (18 – 7)11 = 11(11) = 121 USD
This is the Cournot-Nash solution for oligopoly, found by each firm assuming that the other firm holds its output level constant. The Cournot model can be easily extended to more than two firms, but the math does get increasingly complex as more firms are added. Economists utilize the Cournot model because is based on intuitive and realistic assumptions, and the Cournot solution is intermediary between the outcomes of the two extreme market structures of perfect competition and monopoly.
This can be seen by solving the numerical example for competition, Cournot, and monopoly models, and comparing the solutions for each market structure.
In a competitive industry, free entry results in price equal to marginal cost (P = MC). In the case of the numerical example, PC = 7. When this competitive price is substituted into the inverse demand equation, 7 = 40 – Q, or Qc = 33. Profits are found by solving (P – MC)Q, or πc = (7 – 7)Q = 0. The competitive solution is given in Equation (5.2).
(5.2) Pc = 7 USD/unitQc = 33 unitsπc = 0 USD
The monopoly solution is found by maximizing profits as a single firm.
max πm = TRm – TCm
max πm = P(Qm)Qm – C(Qm)[price depends on total output Qm]
max πm = [40 – Qm]Qm – 7Qm
max πm = 40Qm – Qm2 – 7Qm
∂πm/∂Qm= 40 – 2Qm – 7 = 0
2Qm = 33
Qm* = 16.5
Pm = 40 – 16.5 = 23.5
πm = (Pm – MCm)Qm = (23.5 – 7)16.5 = 16.5(16.5) = 272.25 USD
The monopoly solution is given in Equation (5.3).
(5.3) Pm = 23.5 USD/unit Qm = 16.5 unitsπm = 272.5 USD
The competitive, Cournot, and monopoly solutions can be compared on the same graph for the numerical example (Figure 5.5).
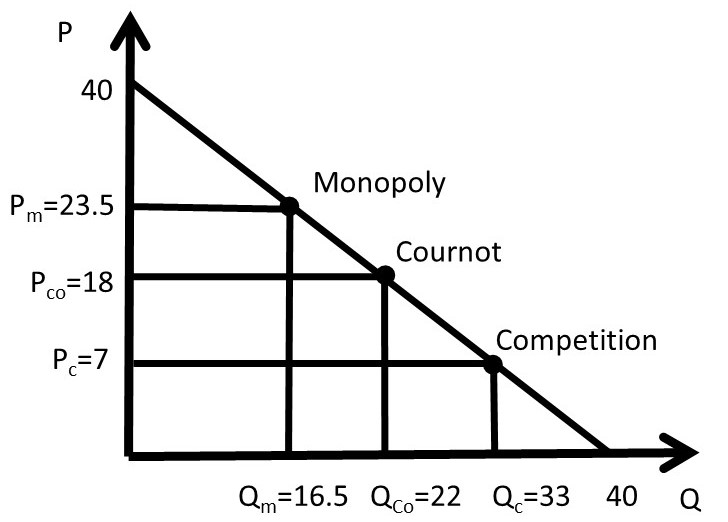
Figure 5.5 Comparisons of Perfect Competition, Cournot, and Monopoly Solutions
The Cournot price and quantity are between perfect competition and monopoly, which is an expected result, since the number of firms in an oligopoly lies between the two market structure extremes.
5.3.3 Bertrand Model
Joseph Louis François Bertrand (1822-1900) was also a French mathematician who developed a competing model to the Cournot model. Bertrand asked the question, “what would happen in an oligopoly model if each firm held the other firm’s price constant?” The Bertrand model is a model of oligopoly in which firms produce a homogeneous good, and each firm takes the price of competitors fixed when deciding what price to charge.
Assume two firms in an oligopoly (a duopoly), where the two firms choose the price of their good simultaneously at the beginning of each period. Consumers purchase from the firm with the lowest price, since the products are homogeneous (perfect substitutes). If the two firms charge the same price, one-half of the consumers buy from each firm. Let the demand equation be given by Qd = Qd(P). The Bertrand model follows these three statements:
(1) If P1 < P2, then Firm One sells Qd and Firm Two sells 0,
(2) If P1 > P2, then Firm One sells 0 and Firm Two sells Qd, and
(3) If P1 = P2, then Firm One sells 0.5Qd and Firm Two sells 0.5Qd.
A numerical example demonstrates the outcome of the Bertrand model, which is a Nash Equilibrium. Assume two firms sell a homogeneous product, and compete by choosing prices simultaneously, while holding the other firm’s price constant. Let the demand function be given by Qd = 50 – P and the costs are summarized by MC1 = MC2 = 5.
(1) Firm One sets P1 = 20, and Firm Two sets P2 = 15. Firm Two has the lower price, so all customers purchase the good from Firm Two.
Q1 = 0, Q2 = 35. π1= 0, π2 = (15 – 5)35 = 350 USD.
After period one, Firm One has a strong incentive to lower the price (P1) below P2.The Bertrand assumption is that both firms will choose a price, holding the other firm’s price constant. Thus, Firm One undercuts P2 slightly, assuming that Firm Two will maintain its price at P2 = 15. Firm Two will keep the same price, assuming that Firm One will maintain P1 = 20.
(2) Firm One sets P1 = 14, and Firm Two sets P2 = 15. Firm One has the lower price, so all customers purchase the good from Firm One.
Q1 = 36, Q2 = 0. π1= (14 – 5)36 = 324 USD, π2 = 0.
After period two, Firm Two has a strong incentive to lower price below P1. This process of undercutting the other firm’s price will continue and a “price war” will result in the price being driven down to marginal cost. In equilibrium, both firms lower their price until price is equal to marginal cost: P1 = P2 = MC1 = MC2. The price cannot go lower than this, or the firms would go out of business due to negative economic profits. To restate the Bertrand model, each firm selects a price, given the other firm’s price. The Bertrand results are given in Equation 5.4.
(5.4) P1 = P2 = MC1 = MC2 Q1 = Q2 = 0.5Qd π1 = π2 = 0 in the SR and LR.
The Bertrand model of oligopoly suggests that oligopolies are characterized by the competitive solution, due to competing over price. There are many oligopolies that behave this way, such as gasoline stations at a given location. Other oligopolies may behave more like Cournot oligopolists, with an outcome somewhere in between perfect competition and monopoly.
5.3.4 Stackelberg Model
Heinrich Freiherr von Stackelberg (1905-1946) was a German economist who contributed to game theory and the study of market structures with a model of firm leadership, or the Stackelberg model of oligopoly. This model assumes that there are two firms in the industry, but they are asymmetrical: there is a “leader” and a “follower.” Stackelberg used this model of oligopoly to determine if there was an advantage to going first, or a “first-mover advantage.”
A numerical example is used to explore the Stackelberg model. Assume two firms, where Firm One is the leader and produces Q1 units of a homogeneous good. Firm Two is the follower, and produces Q2 units of the good. The inverse demand function is given by P = 100 – Q, where Q = Q1 + Q2. The costs of production are given by the cost function: C(Q) = 10Q.
This model is solved recursively, or backwards. Mathematically, the problem must be solved this way to find a solution. Intuitively, each firm will hold the other firm’s output constant, similar to Cournot, but the leader must know the follower’s best strategy to move first. Thus, Firm One solves Firm Two’s profit maximization problem to know what output it will produce, or Firm Two’s reaction function. Once the reaction function of the follower (Firm Two) is known, then the leader (Firm One) maximizes profits by substitution of Firm Two’s reaction function into Firm One’s profit maximization equation. All of this is shown in the following example.
Firm One starts by solving for Firm Two’s reaction function:
max π2 = TR2 – TC2
max π2 = P(Q)Q2 – C(Q2)[price depends on total output Q = Q1 + Q2]
max π2 = [100 – Q]Q2 – 10Q2
max π2 = [100 – Q1 – Q2]Q2 – 10Q2
max π2 = 100Q2 – Q1Q2 – Q22 – 10Q2
∂π2/∂Q2= 100 – Q1 – 2Q2 – 10 = 0
2Q2 = 90 – Q1
Q2* = 45 – 0.5Q1
This is the reaction function of the follower, Firm Two. Next, Firm One, the leader, maximizes profits holding the follower’s output constant using the reaction function.
max π1 = TR1 – TC1
max π1 = P(Q)Q1 – C(Q1)[price depends on total output Q = Q1 + Q2]
max π1 = [100 – Q]Q1 – 10Q1
max π1 = [100 – Q1 – Q2]Q1 – 10Q1
max π1 = [100 – Q1 – (45 – 0.5Q1)]Q1 – 10Q1 [substitution of One’s reaction function]
max π1 = [100 – Q1 – 45 + 0.5Q1]Q1 – 10Q1
max π1 = [55 – 0.5Q1]Q1 – 10Q1
max π1 = 55Q1 – 0.5Q12 – 10Q1
∂π1/∂Q1= 55 – Q1 – 10 = 0
Q1* = 45
This can be substituted back into Firm Two’s reaction function to solve for Q2*.
Q2* = 45 – 0.5Q1 = 45 – 0.5(45) = 45 – 22.5 = 22.5
Q = Q1 + Q2 = 45 + 22.5 = 67.5
P = 100 – Q = 100 – 67.5 = 32.5
π1 = (32.5 – 10)45 = 22.5(45) = 1012.5 USD
π2 = (32.5 – 10)22.5 = 22.5(22.5) = 506.25 USD
We have now covered three models of oligopoly: Cournot, Bertrand, and Stackelberg. These three models are alternative representations of oligopolistic behavior. The Bertand model is relatively easy to identify in the real world, since it results in a price war and competitive prices. It may be more difficult to identify which of the quantity models to use to analyze a real-world industry: Cournot or Stackelberg?
The model that is most appropriate depends on the industry under investigation.
(1) The Cournot model may be most appropriate for an industry with similar firms, with no market advantages or leadership.
(2) The Stackelberg model may be most appropriate for an industry dominated by relatively large firms.
Oligopoly has many different possible outcomes, and several economic models to better understand the diversity of industries. Notice that if the firms in an oligopoly colluded, or acted as a single firm, they could achieve the monopoly outcome. If firms banded together to make united decisions, the firms could set the price or quantity as a monopolist would. This is illegal in many nations, including the United States, since the outcome is anti-competitive, and consumers would have to pay monopoly prices under collusion.
If firms were able to collude, they could divide the market into shares and jointly produce the monopoly quantity by restricting output. This would result in the monopoly price, and the firms would earn monopoly profits. However, under such circumstances, there is always an incentive to “cheat” on the agreement by producing and selling more output. If the other firms in the industry restricted output, a firm could increase profits by increasing output, at the expense of the other firms in the collusive agreement. We will discuss this possibility in the next section.
To summarize our discussion of oligopoly thus far, we have two models that assume that a firm holds the other firm’s output constant: Cournot and Stackelberg. These two models result in positive economic profits, at a level between perfect competition and monopoly. The third model, Bertrand, assumes that each firm holds the other firm’s price constant. The Bertrand model results in zero economic profits, as the price is bid down to the competitive level, P = MC.
The most important characteristic of oligopoly is that firm decisions are based on strategic interactions. Each firm’s behavior is strategic, and strategy depends on the other firms’ strategies. Therefore, oligopolists are locked into a relationship with rivals that differs markedly from perfect competition and monopoly.
5.4 Oligopoly, Collusion, and Game Theory
5.4.1 Collusion and Game Theory
Collusion occurs when oligopoly firms make joint decisions, and act as if they were a single firm. Collusion requires an agreement, either explicit or implicit, between cooperating firms to restrict output and achieve the monopoly price. This causes the firms to be interdependent, as the profit levels of each firm depend on the firm’s own decisions and the decisions of all other firms in the industry. This strategic interdependence is the foundation of game theory.
Game Theory = A framework to study strategic interactions between players, firms, or nations.
A game is defined as:
Game = A situation in which firms make strategic decisions that take into account each others’ actions and responses.
A game can be represented as a payoff matrix, which shows the payoffs for each possibility of the game, as will be shown below. A game has players who select strategies that lead to different outcomes, or payoffs. A Prisoner’s Dilemma is a famous game theory example where two prisoners must decide separately whether to confess or not confess to a crime. This is shown in Figure 5.6.
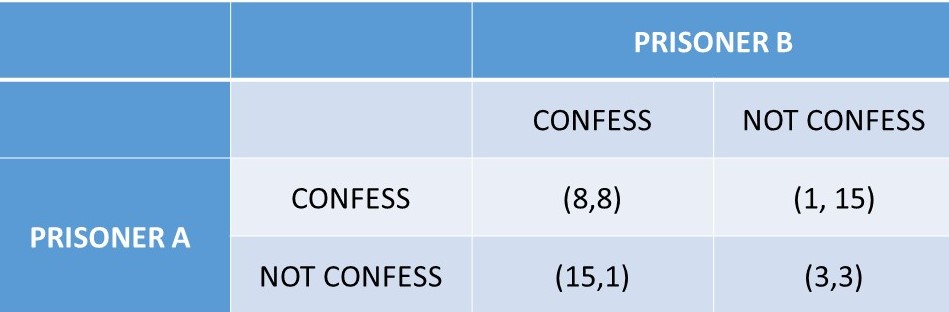
Figure 5.6 A Prisoner’s Dilemma
The police have some evidence that the two prisoners committed a crime, but not enough evidence to convict for a long jail sentence. The police seek a confession from each prisoner independently to convict the other accomplice. The outcomes, or payoffs, of this game are shown as years of jail sentences in the format (A, B) where A is the number of years Prisoner A is sentenced to jail, and B is the number of years Prisoner B is sentenced to jail. The intuition of the game is that if the two Prisoners “collude” and jointly decide to not confess, they will both receive a shorter jail sentence of three years.
However, if either prisoner decides to confess, the confessing prisoner would receive only a single year sentence for cooperating, and the partner in crime (who did not confess) would receive a long 15-year sentence. If both prisoners confess, each receives a sentence of 8 years. This story forms the plot line of a large number of television shows and movies. The situation described by the prisoner’s dilemma is also common in many social and business interactions, as will be explored in the next chapter.
The outcome of this situation is uncertain. If both prisoners are able to strike a deal, and “collude,” or act cooperatively, they both choose to NOT CONFESS, and they each receive three year sentences, in the lower right hand outcome of Figure 5.6. This is the cooperative agreement: (NOT, NOT) = (3,3). However, once the prisoners are in this outcome, they have a temptation to “cheat” on the agreement by choosing to CONFESS, and reducing their own sentence to a single year at the expense of their partner. How should a prisoner proceed? One way is to work through all of the possible outcomes, given what the other prisoner chooses.
A Solution to the Prisoner’s Dilemma: Dominant Strategy
(1) If B CONF, A should CONF (8 < 15)
(2) If B NOT, A should CONF (1 < 3)
…A has the same strategy no matter what B does: CONF.
(3) If A CONF, B should CONF (8 < 15)
(4) If A NOT, B should CONF (1 < 3)
…B has the same strategy no matter what A does: CONF.
Thus, A chooses to CONFESS no matter what. This is called a Dominant Strategy, since it is the best choice given any of the strategies selected by the other player. Similarly, CONFESS is the dominant strategy for prisoner B.
Dominant Strategy = A strategy that results in the highest payoff to a player regardless of the opponent’s action.
The Equilibrium in Dominant Strategies for the Prisoner’s Dilemma is (CONF, CONF). This is an interesting outcome, since each prisoner receives eight-year sentences: (8, 8). If they could only cooperate, they could both be better off with much lighter sentences of three years.
A second example of a game is the decision of whether to produce natural beef or not. Natural beef is typically defined as beef produced without antibiotics or growth hormones. The definition is difficult, since it means different things to different people, and there is no common legal definition. This game is shown in Figure 5.7, where Cargill and Tyson decide whether to produce natural beef.
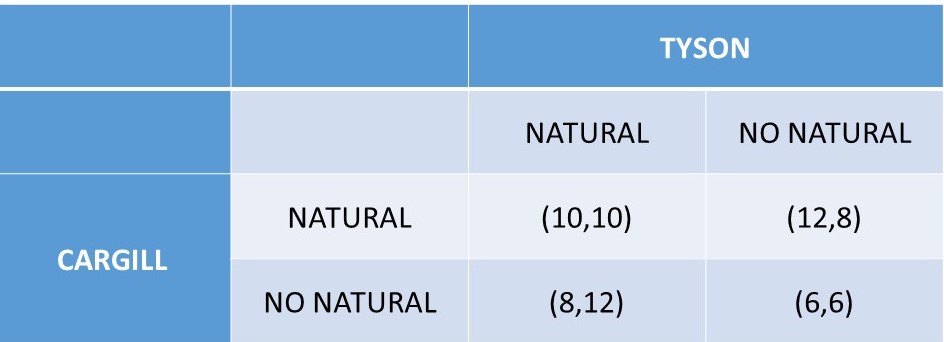
Figure 5.7 The Decision to Produce Natural Beef
There are two players in the game: Cargill and Tyson. Each firm has two possible strategies: produce natural beef or not. The payoffs in the payoff matrix are profits (million USD) for the two companies: (πCargill, πTyson).
Strategy = Each player’s plan of action for playing a game.
Outcome = A combination of strategies for players.
Payoff = The value associated with possible outcomes.
In this game, profits are made from the premium associated with natural beef. If only one firm produced natural beef,
Dominant Strategy for the Natural Beef Game
(1) If TYSON NAT, CARGILL should NAT (10 > 8)
(2) If TYSON NO, CARGILL should NAT (12 > 6)
…CARGILL has the same strategy no matter what TYSON does: NAT.
(3) If CARGILL NAT, TYSON should NAT (10 > 8)
(4) If CARGILL NO, TYSON should NAT (12 > 6)
…TYSON has the same strategy no matter what CARGILL does: NAT.
Both firms choose to produce natural beef, no matter what, so this is a Dominant Strategy for both firms. The Equilibrium in Dominant Strategies is (NAT, NAT). The outcome of this game demonstrates why all beef processors have moved quickly into the production of natural beef in the past few years, and are all earning higher levels of profits. Beef producers have also moved rapidly into organic beef, local beef, grass-fed beef, and even plant-based “beef.”
Prisoner’s Dilemmas are very common in oligopoly markets: gas stations, grocery stores, garbage companies are frequently in this situation. If all oligopolists in a market could agree to raise the price, they could all earn higher profits. Collusion, or the cooperative outcome, could result in monopoly profits. In the USA, explicit collusion is illegal. “Price setting” is outlawed to protect consumers. However, implicit collusion (tacit collusion) could result in monopoly profits for firms in a prisoner’s dilemma. For example, if gas stations in a city such as Manhattan, Kansas all matched a higher price, they could all make more money. However, there is an incentive to cheat on this implicit agreement by cutting the price and attracting more customers away from the other firms to your own gas station. Firms in a cooperative agreement are always tempted to break the agreement to do better.
The Nash Equilibrium calculated for the three oligopoly models (Cournot, Bertand, and Stackelberg) is a noncooperative equilibrium, as the firms are rivals and do not collude. In these models, firms maximize profits given the actions of their rivals. This is common, since collusion is illegal and price wars are costly. How do real-world oligopolists deal with prisoner’s dilemmas is the topic of the next section.
5.4.2 Rigid Prices: Kinked Demand Curve Model
Oligopolists have a strong desire for price stability. Firms in oligopolies are reluctant to change prices, for fear of a price war. If a single firm lowers its price, it could lead to the Bertrand equilibrium, where price is equal to marginal costs, and economic profits are equal to zero. The kinked demand curve model was developed to explain price rigidity, or oligopolist’s desire to maintain price at the prevailing price, P*.
The kinked demand model asserts that a firm will have an asymmetric reaction to price changes. Rival firms in the industry will react differently to a price change, which results in different elasticities for price increases and price decreases.
(1) If a firm increases price, P > P*, other firms will not follow
… the firm will lose most customers, the demand is highly elastic above P*
(2) If a firm decreases price, P < P*, other firms will follow immediately
…each firm will keep the same customers, demand is inelastic below P*
The kinked demand curve is shown in Figure 5.8, where the different reactions of other firms leads to a kink in the demand curve at the prevailing price P*.
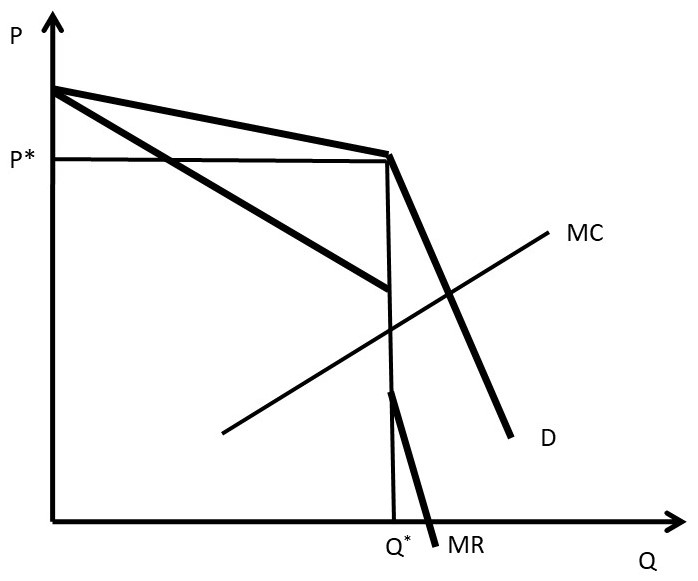
Figure 5.8 Kinked Demand Curve Model
In the kinked demand curve model, MR is discontinuous, due to the asymmetric nature of the demand curve. For linear demand curves, MR has the same y-intercept and two times the slope… resulting in two different sections for the MR curve when demand has a kink. The graph shows how price rigidity occurs: any changes in marginal cost result in the same price and quantity in the kinked demand curve model. As long as the MC curve stays between the two sections of the MR curve, the optimal price and quantity will remain the same.
One important feature of the kinked demand model is that the model describes price rigidity, but does not explain it with a formal, profit-maximizing model. The explanation for price rigidity is rooted in the prisoner’s dilemma and the avoidance of a price war, which are not part of the kinked demand curve model. The kinked demand model is criticized because it is not based on profit-maximizing foundations, as the other oligopoly models.
Two additional models of pricing are price signaling and price leadership.
Price Signaling = A form of implicit collusion in which a firm announces a price increase in the hope that other firms will follow suit.
Price signaling is common for gas stations and grocery stores, where price are posted publically.
Price Leadership = A form of pricing where one firm, the leader, regularly announces price changes that other firms, the followers, then match.
There are many examples of price leadership, including General Motors in the automobile industry, local banks may follow a leading bank’s interest rates, and US Steel in the steel industry.
5.4.3 Dominant Firm Model: Price Leadership
A dominant firm is defined as a firm with a large share of total sales that sets a price to maximize profits, taking into account the supply response of smaller firms. The dominant firm model is also known as the price leadership model. The smaller firms are referred to as the “fringe.” Let F = fringe, or many relatively small competing firms in the same industry as the dominant firm. Let Dom = the dominant firm. The market demand for the good (Dmkt) is equal to the sum of the demand facing the dominant firm (Ddom) and the demand facing the fringe firms (DF).
Ddom = Dmkt – DF
Total quantity (QT) is also the sum of output produced by the dominant and fringe firms.
QT = Qdom + QF
The dominant firm model is shown in Figure 5.9. The supply curve for the fringe firms is given by SF, and the marginal cost of the dominant firm is MCdom. Recall that the marginal cost curve is the firm’s supply curve. The dominant firm has the advantage of lower costs due to economies of scale. In what follows, the dominant firm will set a price, allow the fringe firms to produce as much as they desire, and then find the profit-maximizing quantity and price with the remainder of the market.

Figure 5.9 The Dominant Firm Model
To find the profit-maximizing level of output, the dominant firm first finds the demand curve facing the dominant firm (the dashed line in Figure 5.9), then sets marginal revenue equal to marginal cost. The dominant firm’s demand curve is found by subtracting the supply of the fringe firms (SF) from the total market demand (Dmkt).
Ddom = Dmkt – SF
The dominant firm demand curve is found by the following procedure. The y-intercept of the dominant firm’s demand curve occurs where SF is equal to the Dmkt. At this point, the fringe firms supply the entire market, so the residual facing the dominant firm is equal to zero. Therefore, the demand curve of the dominant firm starts at the price where fringe supply equals market demand. The second point on the dominant firm demand curve is found at the y-intercept of the fringe supply curve (SF). At any price equal to or below this point, the supply of the fringe firms is equal to zero, since the supply curve represents the cost of production. At this point, and all prices below this point, the market demand (Dmkt) is equal to the dominant firm demand (Ddom). Thus, the dashed line below the y-intercept of the fringe supply is equal to the market demand curve. The dominant firm demand curve for prices above this point is found by drawing a line from the y-intercept at price (SF = Dmkt) to the point on the market demand curve at the price of the SF y-intercept. This is the dashed line above the SF y-intercept.
Once the dominant firm demand curve is identified, the dominant firm maximizes profits by setting marginal revenue equal to marginal cost at quantity Qdom. This level of output is then substituted into the dominant firm demand curve to find the price Pdom. The fringe firms take this price as given, and produce QF. The sum of Qdom and QF is the total output QT.
In this way, the dominant firm takes into account the reaction of the fringe firms while making the output decision. This is a Nash equilibrium for the dominant firm, since it is taking the other firms’ behavior into account while making its strategic decision. The model effectively captures an industry with one dominant firm and many smaller firms.
5.4.4 Cartels
A cartel is a group of firms that have an explicit agreement to reduce output in order to increase the price.
Cartel = An explicit agreement among members to reduce output to increase the price.
Cartels are illegal in the United States, as the cartel is a form of collusion. The success of the cartel depends upon two things: (1) how well the firms cooperate, and (2) the potential for monopoly power (inelastic demand).
Cooperation among cartel members is limited by the temptation to cheat on the agreement. The Organization of Petroleum Exporting Countries (OPEC) is an international cartel that restricts oil production to maintain high oil prices. This cartel is legal, since it is an international agreement, outside of the American legal system. The oil cartel’s success depends on how well each member nation adheres to the agreement. Frequently, one or more member nations increases oil production above the agreement, putting downward pressure on oil prices. The cartel’s success is limited by the temptation to cheat. This cartel characteristic is that of a prisoner’s dilemma, and collusion can be best understood in this way.
A collusive agreement, or cartel, results in a circular flow of incentives and behavior. When firms in the same industry act independently, they each have an incentive to collude, or cooperate, to achieve higher levels of profits. If the firms can jointly set the monopoly output, they can share monopoly profit levels. When firms act together, there is a strong incentive to cheat on the agreement, to make higher individual firm profits at the expense of the other members. The business world is competitive, and as a result oligopolistic firms will strive to hold collusive agreements together, when possible. This type of strategic decisions can be usefully understood with game theory, the subject of the next two Chapters.

