Appendix B: Analog Filter Design

Analog Filters

Dwight Day

Appendix B: Analog Filter Design

In this chapter we will be developing filters that employ feedback of the output.  These filters are commonly called Infinite Impulse Response filters (IIR), since the impulse response will extend out to infinity.  To start we will review the design of Analog filters.  Later a translation will be introduced to go from an analog design to a discrete design.

Section A) Filter Specifications.

Before trying to design a filter the first step needs to be to define or describe the type of filter that is to be designed. Defining the response that you will want in your filter will be a function of how it is to be used and is beyond the scope of this discussion. It is sufficient to currently break the types of filter into the three basic types of Low-Pass (LP), High-Pass (HP) and Band-Pass (BP) filters. We will find that each type can be sufficiently described by just a few values.

Part 1) Low-Pass Filter

A sketch of the frequency response of a LP filter is shown in Figure B-1. In this sketch we see that the important values are 1) the upper frequency of the pass band (wp in Figure B.1.), the lower frequency of the stop-band (ws), and the attenuation’s for each band.

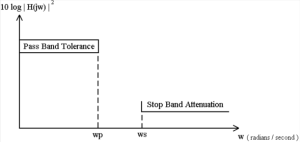
Figure B.1 Sketch of The Frequency Response of A Low-Pass Filter.

Part 2) High-Pass Filter

A sketch of the frequency response of a HP filter is shown in Figure B.2. This type of filter can be characterized in a fashion similar to that of the LP filter, requiring the 1) the upper frequency of the stop band (ws), the lower frequency of the pass-band (ws), and the attenuation’s for each band.

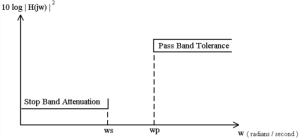
Figure B.2 Sketch of The Frequency Response of A High-Pass Filter.

Part 3) Band-Pass Filter

A band-pass filter is more complex that the LP and HP, but can still be represented by a small set of values. Figure B.3 contains a sketch of the BP frequency response. With the whole specification being set by the end of the lower stop band (wsl), the lower end of the pass band (wpl), the upper end of the pass band (wpu) and the end of the upper stop band (wsu).

Figure B.3 Sketch of The Frequency Response of A Band-Pass Filter.

Section B) Translation to a Normalized Low-Pass Filter

Once the design has been described in one of the previously mentioned forms, each design will be translated to a Normalized Low-Pass (NLP) filter specification. This is done to allow us to identify the proper NLP design that will match our filter once it is translated.

Part 1) Low-Pass Filter to Normalized Low-Pass

The translation that converts a NLP filter, with Laplace variable [latex]\hat s[/latex], to a general LP filter with cutoff or pass-band cutoff frequency of [latex]wp[/latex], is given in formula (B.1)

[latex]\hat s = \frac{s}{wp}[/latex]          (B.1)

This translation will be used to change the H( [latex]\hat s[/latex] ) of the NLP into a LP H(s). However when we translate the NLP, the frequency response is warped to give us our desired response. The frequency warping can be characterized by the following two example points. For [latex]s = \pm j wp [/latex], which translate to [latex]\hat s = \pm j \frac{wp}{wp} = \pm j[/latex]. Also, [latex]s = \pm j ws[/latex], [latex]\hat s = j \frac{ws}{wp}[/latex]. This translation is shown graphically in Figure B.4.

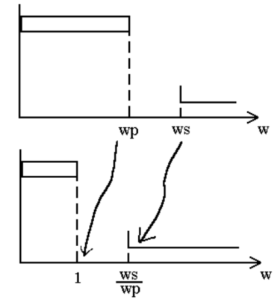
Figure B.4 Low-Pass To Normalized Low-Pass Translation.

Part 2) High-Pass Filter to Normalized Low-Pass

The translation for a HP to NLP is a little more complex, but not that bad. The translation given it equation 2, will take the NLP H(s) and translate it to a HP filter with cutoff of wp.

[latex]\hat s = \frac{wp}{s}[/latex]                (B.2)

Using this translation, [latex]s = +j wp , \hat s \frac{wp}{j wp} = \mp j[/latex] . Note: the sign of s will flip, in other words for s = +j wp, s’ = – j. Also, s = + j ws, s’ = -/+ j wp / ws. This translation is shown graphically in Figure B.5

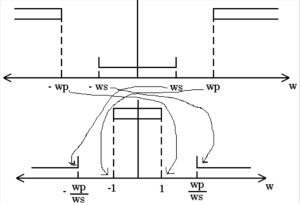
Figure B.5 Sketch of HP to NLP Translation.

Part 3) Band-Pass Filter to Normalized Low-Pass

The third translation is the most complex; however, we are trying to translate from a band pass filter to a NLP, which is no small feat. The translation can be achieved via equation B.3.

[latex]\hat s = \frac{(s^2 + wc^2)}{s wb}[/latex]              (B.3)

where [latex]wc = \sqrt{ wpu * wpl }[/latex] and [latex]wb = ( wpu - wpl )[/latex]  

Again, [latex]\hat s[/latex] is the Laplace variable for the NLP and s the Laplace variable for the BP filter. Let’s consider the four critical frequencies of wpl, wpu, wsl and wsu.
For s = + j wpu,

[latex]\hat s = \frac{(-wpu^2 + wpu * wpl )}{ ( + j wpu ( wpu - wpl ) )} [/latex]

[latex]\hat s = \frac{- wpu ( wpu - wpl ) }{ j wpu ( wpu - wpl ) } [/latex]

[latex]\hat s = \frac{-1 }{ + j } = + j[/latex]

For s = + j wpl,

[latex]\hat s = \frac{-wpl^2 + wpu * wpl }{+ j wpl ( wpu - wpl ) }[/latex]

[latex]\hat s = \frac{- wpl ( wpu - wpl )}{+ j wpl ( wpu - wpl )} [/latex]

[latex]\hat s = \frac{1 }{ + j } = \mp j [/latex]

Note that the sign is reversed in the last equation, in other words for -j wpl, we get +j and for
+j wpl, the result is -j.

For s = + j wsu,

[latex]\hat s = \frac{-wsu^2 + wpu * wpl }{ + j wsu ( wpu - wpl )} [/latex]

[latex]\hat s = \frac{\mp j ( wpl * wpu - wsu2 )}{ wsu ( wpu - wpl ) }   [/latex]

Since wsu > wpu > wpl, the ratio in the previous equation will be negative, which mean no sign reversal will occur.

The last case will be s = + j wsl,

[latex]\hat s = \frac{ -wsl^2 + wpu * wpl}{ + j wsl ( wpu - wpl ) } [/latex]

[latex]\hat s = \frac{\mp j ( wpl * wpu - wsl2 ) }{  wsl ( wpu - wpl ) }[/latex]

However in this case wsl < wpl < wpu, which makes the ratio in the previous equation positive, which means that there will be a sign reversal.
These four cases are then shown graphically in Figure B.6.

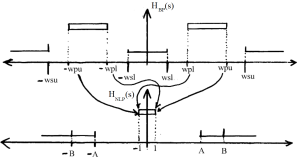
Figure B.6. Sketch of BP to NLP Translation.

Where A is equal to the minimum of [latex]\frac{ wpl * wpu - wsl2}{ wsl ( wpu - wpl ) }[/latex] and [latex]\frac{wpl * wpu - wsu2 }{ wsu ( wpu - wpl )}[/latex], and B is the maximum of these two terms.

In review, it should be pointed out that the translations given by equations 1, 2, and 3 will be used to translate an H(s) for a NLP filter into either an LP, HP or BP filter. So in order to pick the correct NLP filter such that once we translate it into one of the three forms, we obtain the proper filter, we will first translate the specification as was described here.

Section C) Normalized Low-Pass Filter Designs

In the previous section, we showed how to translate our specification into a NLP form. We will describe a couple of common filters that can be used to implement an NLP filter.

Part 1) Butterworth Filter

The first and most popular filter is the Butterworth, which is also called the Maximally Flat filter.  One way to derive the Butterworth filter is to begin with a frequency response of
[latex]| H_n(\omega)^2 | = \frac{1}{1+\omega^{2 n} }[/latex]                 (B.4)
If we substitute s = j w
[latex]| H_n(s)^2 | = \frac{1}{1 + ( (-s^2)^n)}   [/latex]
This can be thought of as an H(s) with poles at [latex]( -s^2 )^n  = -1[/latex],  or
[latex]( s^2 )^n  ( -1 )^n  =  -1[/latex]
and then if we rewrite -1 as [latex]e^{j (2k-1) \pi}[/latex] and [latex](-1)^n  = e^{j \pi n}[/latex] , thus the poles become
[latex]s^{2 n}  =  e^{j( 2k+n-1) \pi} [/latex]
[latex]s_k  =  e^{ j \frac{ 2k+n-1}{2n \pi}[/latex]  with k = 1,2, … , 2n
Consider the case of n=3 then
[latex]s1  =  e^{ j \frac{2}{3} \pi }[/latex] ,  [latex]s2  = e^{ j \pi} = -1[/latex] , [latex]s3  =  e^{ j \frac{4}{3} \pi}[/latex],
[latex]s4  =  e^{j \frac{5}{3} \ pi}[/latex],  [latex]s5 = e^{ j 2 \pi}[/latex], $latex s6 =  e^{ j \frac{7}{3} \pi},
The poles are plotted out in Figure B.7.
Figure B.7 Pole-Zero or S-Plan Plot of a Third-Order Butterworth.
We cannot use these poles directly, since poles in the Right Half Plane (RHP) will cause the system to be unstable ( having an impulse response that goes to infinity ).  This problem develops for the fact that we factored [latex]s^2[/latex] into [latex]\pm s[/latex], but if we only use the -s we will get the same magnitude response.  Thus we need only the poles from the Left Half Plane (LHP).
The NLP Butterworth filter’s H(s) is then
[latex]H( s ) = \sum_{k=1}^{2n} {( \frac{1}{ s-e^{j \pi \frac{2k+n-1}{2n} } } } )[/latex]  (B.5)
For example let n = 3, then
[latex]H( s ) = \frac{1}{ ( (s-e^{j \frac{2}{3}} \pi ) (s-e^{j \pi}) (s-e^{j\frac{4}{3} \pi } ) ) }[/latex]
[latex]H( s ) = \frac{1}{ ( (s-e^{j \frac{2}{3}} \pi ) (s+1) (s-e^{j\frac{4}{3} \pi } ) ) }[/latex]
[latex]H( s ) = \frac{1}{ (s+1)} \frac{1}{( s^2 - s (e^{j \frac{2}{3}} \pi +e^{j\frac{4}{3} \pi } )  + e^{j \frac{2}{3} \pi} * e{j \frac{4}{3} \pi })}[/latex]

Then using [latex]e^{-j \frac{2}{3} \pi} = e^{j \frac{4}{3} \pi }[/latex] we have

[latex]H( s ) = \frac{1}{( s+1)} \frac{1}{( s^2 - 2 RE ( e^{j \frac{2}{3} \pi } )  s + 1 ) }[/latex]
[latex]H(s) = \frac{1}{s+1} \frac{1}{s^2 + s + 1} [/latex]
We will now display the surface of H(s), much like what was done with H(z), using MATLAB.
The following is a MATLAB script file, that creates a sampling of the s plane (complex plane) and the computes the rational function (ratio of polynomials) for H(s)
%===================================================================

limit = 5;
% Set up s plane as real and imaginary parts of s
[x,y] = meshgrid( -2.25:0.05:0, -2.25:0.05:2.25 );
s = x + 1i*y;

% Compute H(s) for third-order Butterworth

H = ( 1 ./ ( s + 1 ) ) .* ( 1 ./ ( s.*s + s + 1 ) );

surf( y,x,min(abs(H3),limit));
view( [ 155 45]);

title (‘H(s) of Third Order Butterworth’);
xlabel( ‘Imaginary’ );
ylabel( ‘Real’);

===================================================================
Figure B.8 Surface Plot of H(s) for NLP Third-Order Butterworth.
Two important features need to be pointed out from this surface plot.  The first is that the three poles are easily visible as the peaks in the plot, and these have been clipped at 5, in order to make some of the other features of the plot more visible.  The poles are evenly distributed on a circle about the origin of the s plane.  The second feature that should be pointed out is the frequency response of the system, which is the H(s) along the imaginary axis.  In the surface plot, we can see that the system is a NLP, since for -1 to 1, H(jw) is ~ 1. Outside this band, the response drops off quickly.  The response is also, well behaved in the pass band, and is as flat as is possible with a third order system, hence Butterworth filter are often called  “Maximally Flat” filters.
Design Equation
The only parameter that can be changed on the NLP Butterworth filter is then the order “n”.  The question then is what order of filter is needed to match the NLP we are needing.  Remember we had a translation or mapping for any filter that would take it to a NLP.  Our mapped NLP will have a cutoff of 1 (rad/sec) and then a stop band frequency (ws) and Stop-Band Attenuation (SBA).  We will now derive the formula required to determine the order n, based on SBA and ws.  First recall from earlier that the frequency response of an nth order Butterworth is
[latex]| H_n (w) |^2 = \frac{1}{ 1 + (w^{2n}) }[/latex]
Substituting in [latex]| H_n (w) |[/latex] = SBA and w = ws, and taking the log of both sides yields,
[latex]2 log | SBA | = log( \frac{1}{1 + (ws^{2n}) } )[/latex]
[latex]2 log |SBA| = log( 1 ) - log( 1 + (ws^{2n})  )[/latex]
[latex]2 log |SBA| \approx - log( ws^{2n} )[/latex]    for ws >> 1
[latex]2 log |SBA| ~  - 2 n log( ws )[/latex]
[latex]n  =  \frac{log |SBA| }{- log( ws )}[/latex]              (B.6)
Thus based on the translated stop frequency and the SBA, we have the design equation (B.6), which can be used to compute n.  To demonstrate the effect of n on the Butterworth response Figure B.9 shows a plot of the NLP frequency response for n = 3 and 5.  It should be noted here that at the cutoff frequency of 1, the response is always at 0.707 (1/ sqrt(2)) .  This response value is often called the half power point or 3 dB point.
Figure B.9 Butterworth Frequency Response for n = 3 and 5.
It should be noted that the use of the log scale allowed us to translate what was an order of a polynomial, to be an algebraic problem.

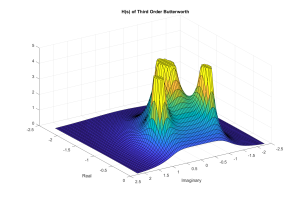
Part 2) Chebyshev or Equal-Ripple Filters

Another class of NLP filters are based on the Chebyshev polynomials. The Chebyshev polynomials are defined as follows,

[latex]C_n(x) = cos( n*arccos( x ) )[/latex] for |x| < 1

and [latex]cosh( n*arccosh( x ) )[/latex] for |x| > 1

These really are polynomials and can be generated by the recursion

[latex]C_{n+1}(x) = 2 x C_n(x) - C_{n-1}(x)[/latex]

From the definition,

[latex]C_0(x) = 1[/latex]

[latex]C_1(x) = x[/latex]

[latex]C_2(x) = 2 x C_1(x) - C_0(x) = 2 x^2 - 1[/latex]

[latex]C_3(x) = 4 x^3 - 3 x[/latex]

We will then define the frequency response of the Chebyshev filter as being

[latex]| H_{n, \epsilon}(w)|^2 = \frac{1}{( 1 + \epsilon^2 C_n^2(w) )[/latex]

where [latex]\epsilon[/latex]e is a scalar with 0 < e < 1
and [latex]C_n(w)[/latex] is the nth order Chebyshev polynomial.

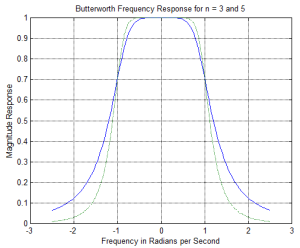
Sketches of [latex]| H_{n, \epsilon}(w)|^2[/latex] for n = 4 and 5, are included in Figure B.10. From the plot we can see that at the cutoff frequency the filter response is not 0.707 as it was with the Butterworth, but rather a function of e. Also the response varies between 1 and [latex]\frac{1}{1+ \epsilon^2}[/latex] in the pass band (0<w<1), which gives rise to these filters other name, Equi-Ripple filters. One final point about the frequency response, if the order of the filter is even, it will have a response of 1/(1+e2) at w = 0, while if it is odd, it will have a response of 1. Also, the number of bumps is equal to the order.

The question is, how do we set e and n to match our NLP. We begin by calculating the

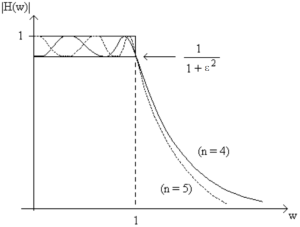
Figure B.10 Frequency Response of Chebyshev NLP Filters.

The ripple in the pass-band of the Chebyshev filter is a function of only e. The larger e, the larger the ripple and the quicker the fall off in the stop band. The Pass-Band Tolerance (PBT) will therefore set the value of e, and is a trade off situation. We will start expressing the PBT in dB, which is 20 log of the ratio of the highest gain ( 1 ) and the lowest ( [latex]\frac{1}{\sqrt{1 + \epsilon^2} }[/latex] )

[latex]PBT = 20 * log10 ( \frac{1}{ \frac{1}{ \sqrt{ 1 + \epsilon^2 } } } ) [/latex]
[latex]PBT = 20 log10 ( sqrt( 1 + \epsilon^2 ) )[/latex]
[latex]PBT = 10 log10 ( 1 + \epsilon^2 )[/latex]
[latex]\epsilon = sqrt( 10PBT/10 - 1 )     [/latex]         (B.7)

Equation B.7 is our first design equation, used to compute [latex]\epsilon[/latex] for the Chebyshev filter.

Next we will determine the order of filter needed. This equation will be derived based on the desired response at the stop frequency.

[latex]SBA = 20* log10 ( \frac{1}{\sqrt{1 + \epsilon^2 C_n^2(ws)}} ) [/latex]

[latex]SBA = -10* log10 ( 1 + \epsilon^2 C_n^2(ws) ) [/latex]

[latex]\frac{SBA}{-10} = log10 ( 1 + \epsilon^2 C_n^2(ws) ) [/latex]

[latex]C_n^2(ws) = \frac{( 10*\frac{SBA}{-10} - 1 )}{ \epsilon^2 } [/latex]

Applying the definition of Cn ,

[latex]cosh( n * arccosh( ws ) ) = \sqrt{ \frac{ ( \frac{10*SBA}{-10} - 1 )}{\epsilon} } [/latex]

Solving for n yields

[latex]n = arccosh( \sqrt( \frac{10*\frac{SBA}{-10} - 1 ) }{e} ) / arccosh( ws )   [/latex]                (B.8)

Equation is the second design equation for the Chebyshev filter.

Now the reason we have defined the Chebyshev filter response as we did was because it can be shown that the polynomial [latex]( 1 + \epsilon^2 C_n^2(ws) )[/latex]will factor to have zeros at

[latex]s_k = a cos( \pi \frac{( 2 k + n - 1 )}{( 2 n ) }) + j b sin( \pi \frac{( 2 k + n - 1 )}{ ( 2 n ) })   [/latex]
where
[latex]a = 0.5 * ( (\sqrt{ 1 + \frac{1}{\epsilon^2} } + \frac{1}{e} )^{\frac{1}{n}}  )- ( \sqrt{ 1 + \frac{1}{\epsilon^2} } + \frac{1}{e} )^{\frac{-1}{n}} )[/latex]
[latex]b = 0.5 * ( ( \sqrt{ 1 + \frac{1}{\epsilon^2} } + \frac{1}{e} )^{\frac{1}{n}} ) + ( \sqrt{ 1 + \frac{1}{\epsilon^2} } + \frac{1}{e} )^{\frac{-1}{n}} )[/latex]

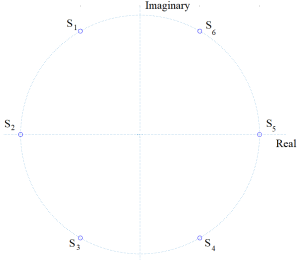
These equations are kind of tedious.  Perhaps a simpler way to view them is as poles which lie on an ellipse with major and minor axis of width [latex]cosh( \frac{1}{n} arccosh(\frac{1}{e} ) )[/latex] and [latex]sinh( \frac{1}{n} arcsinh(\frac{1}{e} ) )[/latex], respectively. Figure B.11 shows a sketch of s-plane and the general shape of the ellipse on which the poles lie.

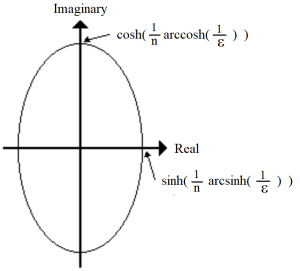
Figure B.11 Plot of s-Plane with Chebyshev Filter Ellipse.

These poles correspond to the scaling of the real and imaginary parts of the Butterworth poles by the factors a and b, respectively. Note at 1 radian/sec, H(jw) is not equal to 0.707 or -3 dB, like the Butterworth, but rather is the ripple value.

Example: Assume a NLP filter with the following parameters is needed (PBT = 1 dB, SBA = -40dB, and ws = 10). Then

[latex]\epsilon = \sqrt{( \frac{10^1}{10} - 1 ) } = 0.5088 [/latex]
[latex]n = \frac{arccosh( \frac{( 10^{\frac{-40}{-10}} - 1 )}{\epsilon^2} ) }{arccosh( 10 )} = 1.99 [/latex]
[latex]n = 2[/latex]

The poles of this filter would now be found as follows,

a = 0.77622 and b = 1.2659
[latex]s1 = 0.77622 cos( \frac{3}{4} \pi ) + j 1.2659 sin( \frac{3}{4} \pi )[/latex]
[latex]s1 = -0.54887 + j 0.89513[/latex]
[latex]s2 = s1* = -0.54887 - j 0.89513 [/latex]
[latex]H(s) = \frac{A}{( (s-s1) (s-s2) ) } = \frac{A}{( s^2 + 1.0977 s + 1.1025 ) [/latex]

Since n is even, we know that

[latex]H(0) = \frac{A }{1.1025}  = \frac{1}{\sqrt{ 1 + \epsilon^2}}   [/latex]

[latex]A = \frac{1.1025}{ \sqrt{ 1 + \epsilon^2 } = 0.9826               [/latex]

[latex]H(s) = \frac{0.9826}{s^2 + 1.0977 s + 1.1025 }       [/latex]

Once again we will view H(s) as a surface in the s-plane.  The following is a MATLAB surface plot and script that shows H(s).  Note the imaginary axis is once again the frequency response.  And since the poles are pulled in closer to the imaginary axis (elliptical nature), there FR ripples more than in the case of the Butterworth.


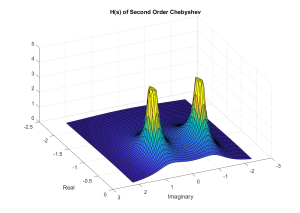
Figure B.12 Surface plot of H(s) for Second-Order 1-dB Ripple Chebyshev NLP Filter.

================================================================

limit = 5;
% Set up z plane as real and imaginary parts of z
[x,y] = meshgrid( -2.25:0.05:0, -2.25:0.05:2.25 );
s = x + 1i*y;

H = 0.9826 ./ ( s.*s + 1.0977 * s + 1.1025 );

surf( y,x,min(abs(H),limit));
view( [ 155 45]);

title (‘H(s) of Second Order Chebyshev’);
xlabel( ‘Imaginary’ );
ylabel( ‘Real’);

================================================================

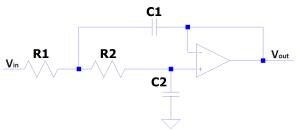
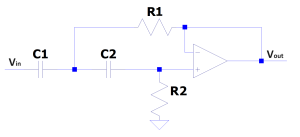
Section D) Back Transformations

Once the NLP design is decided upon, the H(s) must be translated back to the appropriate filter type.  These transformations were described in Section A.  In this section, the transformations will be reiterated here, and shown how the work to convert a NLP to any given filter.

Part 1) NLP to LP.

The transformation was given in equation 1, and here we will apply this transformation to a [latex]H_{nlp}(\hat s)[/latex] to create and [latex]H_{lp}(s)[/latex].
[latex]H_{lp}(s) = H_{nlp}(\hat s) |_{\hat s = \frac{s}{wp} } [/latex]
where wp is the desired cutoff frequency.
Example:  A third order NLP Butterworth is to be translated to have a cut off frequency of 500 Hz or 1000 [latex]\pi[/latex] radians per second.
[latex]H_{lp}(s) = H_{nlp}(\hat s) |_{\hat s=\frac{s}{1000 \pi} } [/latex]
[latex]H_{lp}(s) = \frac{1}{\frac{s}{1000 \pi}+1 } * \frac{1}{\frac{ s^2}{10^6 \pi^2} + \frac{s}{10^3 \pi}+1} [/latex]

Part 2) NLP to HP.

As before the actual transformation was given earlier, and here we will apply it to an [latex]H_{nlp}(\hat s)[/latex] to create the desired filter.
[latex]H_{hp}(s) = H_{nlp}(\hat s) |_{\hat s=\frac{wp}{s}}   [/latex]
Where wp is the cutoff frequency of the desired high-pass filter.
Example: A third-order NLP Butterworth is to be translated to a cut off frequency of 200 radians/second.
[latex]H_{hp}(s)  =  \frac{1}{( \frac{200}{s} + 1 ) } *  \frac{1}{(\frac{40000}{s^2} + \frac{ 200 }{ s } + 1 )}[/latex]
[latex]H_{hp}(s)  = \frac{\frac{s }{200}}{\frac{s}{200} + 1 } *  \frac{ \frac{s^2}{40000}}{\frac{s^2}{40000} + \frac{s}{200} + 1 }[/latex]
In the previous example, we can see that the translated Butterworth still has the set of poles distributed around in a circle, but a set of three zeros have been added at the origin.  This force the response to zero here, and then the zeros and poles compensate each other at high frequencies.

Part 3) NLP to BP.

The last transformation will be the NLP to Band-Pass fitler as given in equation 3, and here we will apply this transformation to a Hnlp(s’) to create and Hlp(s).
[latex]H_{bp}(s) = H_{nlp}(\hat s) |_{\hat s=\frac{s*s + wpu*wpl}{s * (wpu-wpl)} } [/latex]
where wpu is the desired upper cutoff frequency
     and wpl is the desired lower cutoff frequency.
Example:  Again we will translate a third order NLP Butterworth; however, this time we will be translating to a BP, with wpl = 100 and wpu = 1000 radians per second.
[latex]H_{bp}(s)  =  \frac{1}{frac{s^2 + 10^5}{(s*900)} +1} *\frac{1}{(\frac{s^2 + 10^5 }{(s 900)^2} + \frac{s^2 + 10^5} {s 900}+ 1 }[/latex]
[latex]H_{bp}(s)  = \frac{\frac{s}{10^5} }{ ( \frac{s^2}{9*10^8 } + \frac{s}{10^5} + 1 ) }  *\frac{ (9900 s)^2 }{( s^4 +  9* 10^3 s^3 + 2*10^6 s^2 + 9*10^7 s + 10^{10} + 900^2}   [/latex]
This last equation will need to be factored in order to be implemented in a reasonable fashion.

Part 4) Implementation

Once a valid H(s) has been derived for our filter, there are a variety of ways to implement the filter.  A classic and straight forward approach is to use the Sallen-Key topology.  In this case H(s) should be broken into second order pairs, which occurs naturally in the creation of the transfer function.  Each second order pair can be implemented using one of the following circuits.
Figure B.13 Sallen-Key Circuit for Low-Pass Second Order Pair.
The transfer function for the circuit in Figure B.13 is given as
[latex]H(s) = \frac{\omega_o}{s^2+ 2\alpha*s+\omega_o^2}[/latex]
where [latex]\omega_o = \frac{1}{sqrt( R1*R2*C1*C2 )}[/latex] and [latex]2 \alpha = \frac{1}{C1} * \frac{R1+R2}{R1*R2}[/latex]
The four components of R1, R2, C1 and C2 give sufficient flexibility to create any second order system that is needed.
Figure B.14 Sallen-Key Circuit for High-Pass Second Order Pair.
The transfer function for the circuit in Figure B.14 is given as
[latex]H(s) = \frac{s^2}{s^2+ 2\tau*\omega_0*s+\omega_o^2}[/latex]
where [latex]\omega_o = \frac{1}{sqrt( R1*R2*C1*C2 )}[/latex] and [latex](2\tau*\omega_0) = \frac{1}{C1} * \frac{C1+C2}{R1*C1*C2}[/latex]
Again the four components of R1, R2, C1 and C2 give sufficient flexibility to create any second order system that is needed.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Appendix B: Analog Filter Design Copyright © 2023 by Dwight Day is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book