10 Look Before You Leap Demystifying Quantum Computing’s Enigmatic Frontier (Sharkey)

“Dive into the quantum chaos with me, where the wild frontiers of possibility clash with the raw power of human creativity. Chapter 10: Look Before You Leap: Unraveling the complexities of quantum computing blasts through the noise to reveal a rebellion of innovation. We are challenging the boundaries where computation meets its match and transforms. This chapter cranks up the volume on transformative paths, spotlighting how a deep dive into the nitty-gritty of quantum mechanics can revolutionize our future and kick open the doors to radical advancements for humanity.”

-Mrs. Keeper L. Sharkey, PhD (author)

Preface

This chapter delves into classical computing and its limitations, setting the stage for the transformative principles of quantum mechanics (QM) foundational to quantum computing (QC). It explores core concepts such as qubits, superposition, entanglement, and quantum gate operations, laying the groundwork for understanding QC’s revolutionary potential. The discussion extends to various QC modalities, including superconducting qubits, trapped ions, and photonic qubits, highlighting their unique advantages, challenges, and current states. A thorough exploration of quantum algorithms, such as Shor’s algorithm for integer factorization and Grover’s algorithm for search problems, demonstrates their vast applications across finance, healthcare, materials science, and cryptography and their capability to solve complex problems like the Traveling Salesman Problem and portfolio optimization. Additionally, this chapter considers the broader societal implications, addressing ethical considerations, privacy issues, and the democratization of technology. It evaluates the impact of QC on global challenges like climate change, healthcare, and cybersecurity and underscores its role in advancing scientific research and drug discovery. Concluding with crucial insights and takeaways, the chapter emphasizes the transformative potential of QC for humanity, advocating for responsible innovation and ethical stewardship. It invites readers to engage with and contribute to the ongoing development and adoption of QC technologies, fostering a collective effort to shape the future, scoring the need to eliminate misconceptions, and teaching what is needed to improve the industry holistically.

Introduction

In the realm of computing, specific problems loom as nearly insurmountable peaks, daunting in their complexity and scale. These include factorial-dependent calculations for large numbers and NP-hard problems, which require computational power that grows exponentially with input size. Classical computers, limited by binary precision and sequential processing, struggle with these real-world issues—ranging from optimizing logistics networks to decrypting secure communications. These challenges also intriguingly intersect with fields such as origami folding, where the sequence of folds represents complex problem-solving, and space travel, where trajectory optimizations involve factorial growth in computational demands.

Enter QC: a revolutionary approach leveraging the unique properties of QM. Unlike classical computing based on binary states, QC uses qubits that can exist in multiple states simultaneously due to superposition and are interconnected through entanglement. This technology promises to perform calculations at unprecedented speeds and tackle complex optimizations and simulations beyond current capabilities.

As we embark on this QC revolution, this introduction serves as a gateway to understanding its underlying principles and transformative potential. We will explore QM foundations, examine various QC modalities like superconducting qubits and trapped ions, and investigate the profound impact of quantum algorithms across multiple sectors, including finance and healthcare. We will also discuss the specific enhancements QC brings to financial modeling and risk management alongside broader societal implications such as ethical considerations and technology democratization. Concluding with future challenges and prospects, this journey aims to illuminate how QC not only advances technology but also has the potential to reshape our world.

Computing: Classical Computing vs. QC and Everything Else in Between

Understanding classical computing serves as the foundational stepping stone toward comprehending the revolutionary paradigm of QC. Classical computing principles, rooted in binary logic and sequential processing, provide the basis for appreciating the fundamental challenges and limitations that aim to transcend. By grasping concepts such as algorithms, data structures, and computational complexity within the classical computing framework, individuals gain insight into the computational problems that QCs seek to solve more efficiently. Moreover, an understanding of classical computing elucidates the significance of quantum enhancements, showcasing how quantum algorithms can revolutionize tasks such as optimization, cryptography, and simulation. Thus, delving into classical computing not only equips us with the necessary knowledge to appreciate the QC landscape but also underscores the transformative potential of quantum technologies in shaping the future of computation and innovation.

Foundations of Classical Computing

Classical computers, which encompass everything from early calculating machines to modern supercomputers, operate using bits as the basic unit of information. These bits are binary, existing in one of two possible states: 0 or 1. The operations of classical computers—whether they involve the most straightforward calculations or complex simulations—are ultimately reducible to manipulations of these binary bits through logical gates in a deterministic, sequential fashion.

Processing Power and Limitations

While classical computers have transformed society through their ability to automate calculations and process information at speeds unattainable by human capacity, they have inherent limitations. The binary nature of bits means that each bit represents a single state at any one time, which restricts the complexity of problems they can efficiently solve. For tasks involving large data sets or requiring exponential scaling—like factoring large integers or simulating large molecular structures—classical computers either require impractical amounts of time or consume excessive energy.

Approaching Computational Limits

As we push classical computers to tackle more complex or data-intensive problems, we encounter physical and practical limits. Moore’s Law, which predicted the doubling of transistors on a chip approximately every two years, is reaching its physical limitations due to quantum effects that occur at atomic scales. Additionally, problems in fields such as cryptography, climate modeling, and logistics often present computational demands that outstrip what can be practically managed with current technology.

MOORE’S LAW

Moore’s Law, named after Gordon Moore, co-founder of Intel, is a prediction that has significantly influenced the electronics industry and technological advancement. In 1965, Moore observed that the number of transistors on a microchip doubled approximately every two years while the cost of computers was halved. This observation has held for several decades, driving the exponential increase in computing power and the reduction in the size and cost of electronic devices. Moore’s Law is not a law of physics but rather an empirical relationship and industry guideline that has spurred continuous innovation and development within the technology sector. It has enabled the proliferation of technology in everyday life, from personal computers and smartphones to sophisticated healthcare equipment and smart home devices. However, as transistor sizes approach the atomic scale, physical limitations threaten to slow this pace of progress, challenging the industry to find new ways to sustain technological growth and innovation.

MURPHY’S LAW

In the context of classical computing, Murphy’s Law—”anything that can go wrong, will go wrong, and at the worst possible time”—serves as a cautionary principle akin to entropy and the second law of thermodynamics, reminding us of the inherent unpredictability and potential vulnerabilities in technological systems. This adage is named after Captain Edward A. Murphy, Jr., an American aerospace engineer who worked on safety-critical systems. He was involved in high-speed rocket sled experiments during the 1940s, which were designed to test human tolerance for speed and deceleration. As we increase our reliance on classical computers, the impacts of failures become more critical, particularly in high-stakes environments such as financial markets, healthcare systems, and critical infrastructure. These failures can range from hardware malfunctions to software bugs and security breaches, each capable of occurring at the least opportune moments, causing not just operational disruptions but also significant financial and social repercussions. Acknowledging this law encourages the design of more robust, fault-tolerant systems and highlights the importance of contingency planning in our ever-growing digital landscape. It also reinforces the pursuit of QC to mitigate some of these risks, offering new avenues for error correction and enhanced security protocols that are less susceptible to the whims of Murphy’s Law.

Setting the Stage for QC

These limitations illuminate the need for a new kind of computing. QC promises to break through these barriers by leveraging the principles of QM, offering not just incremental improvements but exponential leaps in processing power. This shift can potentially revolutionize fields by enabling the calculation of what today seems impossible, paving the way for advancements beyond our imagination.

The evolution of classical computing has been a cornerstone of modern civilization, profoundly influencing every aspect of human life. From global communication networks and medical advancements to how we learn, shop, and entertain ourselves, the capabilities of classical computers have reshaped the social, economic, and cultural landscapes. However, as we navigate increasingly complex global challenges—such as climate change, population growth, and the need for sustainable development—the limitations of classical computing present significant hurdles. By pushing the boundaries of what is computationally feasible, we prepare the ground for QC to continue this trajectory of technological empowerment and accelerate our ability to address and solve pressing global issues. This transition underscores the importance of computational power in driving human progress and the continuous need for technological innovation that adheres to ethical standards and promotes the well-being of all. 

Enter in QM

Quantum Mechanics (QM) is a fundamental theory in physics that describes nature at the minor scales of energy levels of atoms and subatomic particles. Central to QM are the ideas of wave-particle duality, the Heisenberg uncertainty principle, and quantum superposition. These principles challenge our classical intuitions about how particles behave and interact, suggesting that particles can exist in multiple states simultaneously and that observing a system inevitably alters its state.

In chemistry, QM explains the structure and behavior of atoms and molecules. It is essential for understanding chemical bonding, the arrangement of electrons in atoms and molecules, and how chemical reactions occur. Quantum principles help chemists predict the properties of molecules, their reactivity, and how they absorb and emit light, providing a deeper understanding of phenomena from simple chemical reactions to complex mechanisms in biochemistry. QM also revolutionizes our understanding of light and its interaction with matter. The dual nature of light as both waves and particles (photons) explains phenomena such as interference and diffraction, which are central to many modern technologies, including lasers, microscopes, and semiconductor devices. Furthermore, the quantum description of light has led to the development of quantum field theory, which seeks to unify the fundamental forces of nature, suggesting profound connections between light, energy, and the universe’s basic structure.

QM has not only transformed our understanding of matter and energy on the microscopic scale but also has implications for the cosmological scale, influencing theories about the origin and evolution of the universe. Concepts from QM are integral to the study of black holes, the behavior of particles at extreme densities and temperatures, and the nature of dark matter and dark energy, which compose most of the universe’s mass-energy content.

The Postulates of QM

These quantum principles are not merely theoretical curiosities; these are the very tools that make QC possible – not LAW (Levine, 2014). QCs leverage superposition and entanglement to perform computations in ways that are fundamentally different from classical computers, promising new realms of processing power and efficiency. As such, QM is not only a pivotal chapter in the story of physics and chemistry but also the foundation upon which the future of computing is being built. Here is a summary of the fundamental postulates of QM, which form the foundational principles governing the behavior of particles at the quantum level:

1. State Postulate: The state of a quantum system (QS) is entirely described by a wave function (WF), denoted as ψ, which encodes the probabilities of all possible outcomes of measurements made on the system. The total WF is a complex-valued function of the (spatial and spin) coordinates of the particle, including time.
2. Superposition Principle: Any linear combination of possible states (or WFs) of a QS is itself a potential state. This principle allows QSs to be in multiple states simultaneously, a phenomenon known as superposition.
3. Quantum Measurement Postulate: The act of measuring a QS affects its state. According to this postulate, the outcome of a quantum measurement is one of the eigenvalues of the operator associated with the observable being measured, and the probability of obtaining a specific eigenvalue is given by the square of the amplitude of the WF in the corresponding eigenstate (Born rule).
4. Time Evolution Postulate: The time evolution of a QS is described by the Schrödinger equation. This postulate specifies how the WF of a QS changes over time, dictating that the evolution is unitary and deterministic under isolated conditions.
5. Quantum Entanglement Postulate: When two QSs interact and then separate, the description of their states may become entangled, meaning the state of each system can no longer be described independently of the state of the other. Measurements performed on one system can instantaneously affect the state of the different systems, a phenomenon that Albert Einstein famously referred to as “spooky action at a distance.”

These postulates lay the groundwork for the quantum theory, providing a framework that explains a wide range of phenomena, from the microscopic behavior of particles in an atom to the properties of solids and the fundamental aspects of chemistry. (Khan, Sharkey, & & Chancé, 2022)

In QM, {bra-ket }notation is a powerful mathematical formalism used to describe the states of QSs and the operations performed on them. The notation consists of two elements: the “bra” ⟨ψ| and the “ket” |φ⟩, where ψ and φ represent quantum states using Greek letters. The bra-ket notation elegantly captures the concept of duality between vectors and dual vectors (or “bra” and “ket” vectors), allowing for intuitive representation and manipulation of quantum states and operators. 

DIRAC (BRA-KET) Notation

Paul Dirac’s work laid the foundation for the field of quantum physics and helped to predict the existence of particles like the positron, which was later discovered experimentally in 1932. His insights and theories have had a profound and lasting impact on the development of particle physics and the understanding of the fundamental forces of nature. In recognition of his significant contributions, Dirac was awarded the Nobel Prize in Physics in 1933, alongside Erwin Schrödinger, for the discovery of new productive forms of atomic theory. Throughout his career, Dirac was known for his precise and formal approach to physics, often focusing on mathematical beauty and simplicity, which he believed were guides to fundamental truths about nature. His legacy includes not only his contributions to the theoretical framework of particle physics but also his influence on generations of physicists who have built upon his ideas. He is credited with introducing the bra-ket notation.

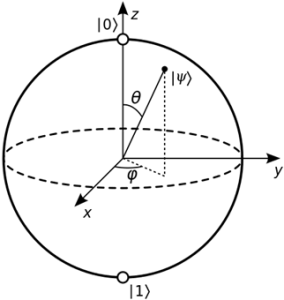
The ket |φ⟩ represents a quantum state in a Hilbert space, where each component corresponds to the amplitude or probability of finding the system in a particular state. For example, in a qubit system, |0⟩ and |1⟩ represent the basis states corresponding to the classical bit states 0 and 1, respectively. Superposition states, such as |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers representing probability amplitudes, can also be represented using ket notation.

On the other hand, the bra ⟨ψ| represents the complex conjugate transpose of the ket |ψ⟩. It represents the dual vector corresponding to the state |ψ⟩. By taking the inner product of a bra and a ket, denoted as ⟨φ|ψ⟩, one obtains a complex number that represents the probability amplitude for transitioning from state |ψ⟩ to state |φ⟩. This inner product captures the overlap between the two quantum states and is fundamental to QM, playing a crucial role in the calculations of probabilities and expectation values.

Bra-ket notation is intimately related to QM, providing a concise and elegant language for describing quantum states, operations, and measurements. It enables physicists and researchers to express complex quantum phenomena clearly and intuitively, facilitating the development and understanding of quantum algorithms, quantum circuits, and QSs. Moreover, [bra-ket] notation serves as a foundational tool for the formulation and solution of problems in QM, quantum information theory, and QC, highlighting its central importance in the study of the quantum world.

HILBERT Space

A Hilbert space is a mathematical concept used in QM to represent the state space of a QS. It is a complex vector space equipped with an inner product, which allows for the measurement of distances and angles between vectors. Hilbert spaces are essential for describing the states of QSs, as well as the operations and transformations that can be applied to them. Formally, a Hilbert space is defined as a complete inner product space, meaning that it is equipped with an inner product (a function that takes two vectors and returns a complex number) and is also complete with respect to the norm induced by this inner product. Completeness implies that every Cauchy sequence (a sequence in which the elements become arbitrarily close to each other as the sequence progresses) in the space converges to a limit within the space itself. In the context of QM, the Hilbert space represents the set of all possible states of a QS.

The Cauchy sequence is named after Augustin-Louis Cauchy, a French mathematician who was a pioneering figure in the development of analysis during the early 19th century. Cauchy was born on August 21, 1789, and made significant contributions to many areas of mathematics, including calculus, complex analysis, and number theory. He was particularly influential in establishing the rigor that is now standard in mathematical analysis. One of Cauchy’s notable contributions is the formal definition of a limit and the introduction of what we now call the Cauchy sequence. A Cauchy sequence is a sequence where the terms become arbitrarily close to each other as the sequence progresses. More formally, a sequence (𝑥𝑛) of real numbers is called a Cauchy sequence if, for every positive real number 𝜖, there exists a positive integer 𝑁 such that for all integers 𝑚, 𝑛≥N, the distance ∣𝑥𝑚−𝑥𝑛∣<𝜖. This concept is fundamental in the analysis of convergence in metric spaces, particularly because it allows for the discussion of convergence without explicitly referencing limits.

Each vector in the Hilbert space corresponds to a quantum state, and the inner product between two vectors represents the probability amplitude or overlap between those states. Quantum operators, such as observables and transformations, are represented by linear operators acting on vectors in the Hilbert space. The dimensionality of a Hilbert space corresponds to the number of degrees of freedom or independent parameters required to specify the quantum state of the system. For example, a single qubit system in QC is typically represented by a two-dimensional Hilbert space, while systems with multiple qubits span higher-dimensional Hilbert spaces.

Cauchy’s work laid much of the groundwork for the theories we now have in mathematical analysis and was pivotal in transitioning from the intuitive notions of calculus to more rigorous and systematic approaches. His definitions and theorems are still fundamental in mathematics today, especially in subjects dealing with real numbers, series, and functions. Cauchy’s influence extends beyond just sequences; he also contributed significantly to the development of complex function theory, differential equations, and determinants. His rigorous approach has shaped modern mathematical analysis, making his work essential to both pure and applied mathematics.

Angular Momentum

Angular momentum is a fundamental concept in QM that is relevant to the understanding of qubits and QC. In classical mechanics, angular momentum is a physical quantity that represents the rotational momentum of an object in motion around a point. It is a vector quantity calculated as the cross product of the position vector and the linear momentum vector. This concept is crucial for understanding rotational dynamics in macroscopic systems, such as planets orbiting the sun or a spinning top. Angular momentum in classical mechanics is conserved in a closed system, meaning it remains constant if no external torques are applied.

In QM, angular momentum retains its fundamental role as a measure of rotational motion, but it is quantized, meaning it can only take on specific discrete values. This quantization is one of the stark differences between classical and quantum descriptions. Unlike in classical mechanics, where angular momentum can vary continuously, quantum angular momentum is inherently quantized. For a given system, the total angular momentum and its component along any axis (usually denoted as the z-axis) can only take on certain discrete values, typically in integer or half-integer multiples of the reduced Planck constant (ℏ). The Planck constant is a crucial value in QM that describes the quantization of energy, momentum, and angular momentum at microscopic scales. Its value is approximately 6.62607015×10−34 joule-seconds, making ℏ approximately 1.0545718×10−34 joule-seconds.

Moreover, angular momentum conservation principles play a role in certain quantum algorithms and quantum simulations. For example, quantum algorithms (QA) for simulating molecular dynamics or solving certain optimization problems may involve the conservation of angular momentum as a constraint or as a property of the QS being modeled. Understanding these connections can provide insights into the underlying physics of QC and aid in the design and analysis of QA and devices.

Magnetic Spin

Spin is a fundamental quantum property of particles akin to intrinsic angular momentum; however, it does not have a classical counterpart. It is an inherent characteristic of elementary particles, including electrons, protons, and neutrons, providing them with a magnetic moment, which is the magnetic strength and orientation of a particle. Unlike orbital angular momentum, which arises from a particle’s motion through space, spin is an intrinsic form of spin momentum.

In QM, spin is quantized, meaning that it can only take on certain discrete values. For electrons, which are the primary concern in many practical applications, the spin quantum number s is 1/2. This quantization results in two possible spin states for electrons:

• spin-up (+1/2​) denoted as ∣↑⟩
• spin-down (−1/2​), denoted as ∣↑⟩

It is important to mention that electrons are “fermionic” particles, i.e., fermionic particles have half-integer quantization. Bosons, on the other hand, have integer spin quantization.

The measurement of spin-1/2 along any spatial axis can yield only one of two values: +ℏ/2 or −ℏ/2 for particles like electrons. The symbol ℏ (pronounced “h-bar”) is a fundamental constant in physics, particularly in QM, representing the reduced Planck constant (ℎ) and is defined as:

ℏ = h/2πℏ                                               Equation 10-1

This simplifies many formulas in QM, especially those involving angular momentum or action in units of radians. When not measured, an electron’s spin state can be a superposition of both up and down states, expressed as 𝛼∣↑⟩+𝛽∣↓⟩, where 𝛼 and β are complex numbers that describe the probability amplitudes of finding the electron in either state upon measurement. In other words, 𝛼 and β represent the ratio of spin-up and spin-down.

The interaction of spin with magnetic fields is crucial for many technologies. In the presence of a magnetic field, the magnetic moments associated with spin tend to align with the field, resulting in distinct energy states depending on the spin orientation. This principle is exploited in magnetic resonance imaging (MRI) and electron spin resonance (ESR) spectroscopy. The energy difference between the spin states in a magnetic field can be probed by electromagnetic radiation, typically in the radiofrequency range for MRI.

Spin is also central to the Pauli Exclusion Principle (PEP), which states that no two fermions (particles like electrons) can occupy the same quantum state within a QS simultaneously. This principle explains a wide range of physical phenomena, from the structure of atoms and the periodic table to the behavior of electrons in metals and semiconductors. PEP represents a factorially dependent problem.

Look Before You Leap: Symmetry Operations of the Total Wave Function and the Generalized Pauli Exclusion Principle

Wolfgang Pauli formulated the Exclusion Principle in 1925. This fundamental principle of QM states that no two identical fermions (particles with half-integer spin, such as electrons, protons, and neutrons) can occupy the same quantum state simultaneously within a QS. This principle is critical to understanding the structure of atoms and molecules, as it explains the arrangement of electrons in atomic orbitals and the properties of particles in the periodic table. Pauli’s Exclusion Principle has profound implications across physics and chemistry, influencing everything from the stability of matter to the types of chemical bonds that atoms can form. It was for this discovery and his formulation of the principle that Pauli was awarded the Nobel Prize in Physics in 1945.

As initially formulated, the Pauli Exclusion Principle states that no two identical fermions (particles like electrons) may occupy the same spin-quantum state simultaneously. This principle introduces complex symmetrical considerations when determining the electronic structure of atoms and molecules, which is essential for predicting chemical behavior and bonding. The concept of bosons came later with the development of quantum statistics. Bosons are named after the Indian physicist Satyendra Nath Bose, whose work on photon statistics was sent to Albert Einstein in the mid-1920s. Einstein extended Bose’s theory to atoms, which played a crucial role in the development of the theory of Bose-Einstein condensation. The term “boson” and the classification of particles into bosons and fermions (after Enrico Fermi) came about as QM matured, which was after Pauli’s initial formulation of his exclusion principle.

Bosons, which include particles such as photons, gluons, and certain atoms (like those used in Bose-Einstein condensates), are defined by their integer spin values (s = 0, 1, 2, 3, …). This integral spin leads to their characteristic behavior under Bose-Einstein statistics, allowing them to occupy the same spin-quantum state without restriction. Unlike fermions, which are subject to the Pauli Exclusion Principle preventing any two identical fermions from occupying the same quantum state, bosons can exhibit spin-degeneracy, where multiple particles exhibit the same set of quantum numbers.

The Generalized Pauli Exclusion Principle (GPEP) is an extension of Pauli’s original theory to the total Wave Function (WF) describing a system (both fermionic and bosonic) and the related symmetry requirements for both the spin and spatial functions that comprise the total WF. The mathematics of the GPEP is beyond the scope of this chapter. For those readers interested in delving into the derivations of Fermions, Bosons, their antisymmetric and symmetric spatial functions, and spin characteristics, consult the chapter author’s many presentations and writings on the subject. The main points are that QC is complex and that complexity works in our favor to solve many problems for humanity. Life is complex. It takes speed, accuracy, and complex solutions to improve our lot. QC is a harbinger of the future. Classical computing systems will be a thing of the past, like floppy disks, Betamax, home phones, fax machines, typewriters, VHS movies, pagers, overhead projectors, and rotary telephones.

NP-Hard Problems

Another area where classical computing meets significant challenges is in solving problems involving symmetry operations under the generalized PEP, which is crucial in quantum chemistry and physics. This symmetry operation is a factorial-dependent, NP-hard problem and grows exponentially with system size. Many approximations are made in the field of computational chemistry, rendering most simulations of chemical systems to be inaccurate. Depending on the level of truncation, we can only hope to become increasingly more accurate. It is a cautionary tale in academia because this generalized PEP is not taught to the extent it ought to be.

Bridging QM and QC

The core concepts of QC are directly rooted in the foundational postulates of QM, demonstrating a profound application of these principles in technology. The behavior of qubits—QC’s fundamental units—is dictated by the quantum state postulate, enabling them to exist in multiple states simultaneously through superposition. This capability is further enhanced by the quantum entanglement postulate, which allows linked qubits to share state information instantaneously across distances, a critical feature for QA. Quantum gates, analogous to classical logical gates but operating under the rules of QM, manipulate qubit states in line with the time evolution postulate, ensuring coherent and reversible operations essential for quantum calculations. These interactions are designed to exploit phenomena such as superposition and entanglement to perform computations that are not only faster but fundamentally different from those possible with classical computers. As we delve into the specifics of how QCs leverage these interactions, it becomes clear that understanding the postulates of QM is crucial for appreciating the full potential and the innovative operations of QC.

Core Concepts of QC

At the heart of QC lies the quantum bit, or qubit, which is the basic unit of quantum information. Unlike classical bits, which are strictly binary and exist as either 0 or 1, qubits can exist simultaneously in multiple states due to quantum superposition. This allows a qubit to be in a state representing both 0 and 1 at the same time, which is expressed mathematically as α∣0⟩ + β∣1⟩, where α and β are complex numbers that describe the probability amplitudes of these states.

Superposition is a principle where a QS can be in multiple states at once. For qubits, this means being in a state that is a combination of both 0 and 1, vastly increasing the potential computational power. When a qubit in superposition is measured, it ‘collapses’ to one of the base states (0 or 1), and the outcome is probabilistic based on the coefficients α and β.

Entanglement is a uniquely quantum phenomenon where qubits become interconnected such that the state of one (no matter how far apart they are) cannot be described without full knowledge of the state of the other. This linkage allows QCs to perform complex calculations more efficiently by enabling instantaneous communication of state information between entangled qubits.

In classical computing, bits are manipulated via logical gates. In QC, quantum gates operate on qubits and are used to perform computations. Quantum gates are reversible and are represented by unitary matrices, ensuring that the transformations they apply preserve the probabilistic nature of qubits’ states. These gates manipulate the probabilities and phases of the states of qubits, allowing for the execution of algorithms that can solve problems in ways classical computers cannot.

Quantum circuits are sequences of quantum gates designed to perform specific computational tasks. Like classical circuits, they take a set of input states (qubits) and transform them into output states via a series of gate operations. However, because of superposition and entanglement, quantum circuits can process a vast number of possible inputs simultaneously. 

Quantum circuits are sequences of quantum gates designed to perform specific computational tasks. Like classical circuits, they take a set of input states (qubits) and transform them into output states via a series of gate operations. However, because of superposition and entanglement, quantum circuits can process a vast number of possible inputs simultaneously.

One of the significant challenges in QC is maintaining the integrity of qubits over time. Quantum decoherence occurs when qubits lose their quantum behavior, typically due to unintended interactions with the environment. This can disrupt computations by causing the qubits to lose their superposition and entanglement properties, reverting them to classical states. Developing methods to protect against decoherence is a critical area of research in making QC practical.

QC promises a paradigm shift in processing power through its unique capabilities, such as superposition and entanglement. Unlike classical computers, QCs excel in handling vast computational spaces, enabling them to tackle specific types of problems that classical systems find intractable. These include complex optimizations, simulations of quantum physical processes, and specific cryptographic challenges where QC can provide exponential speedups.

Furthermore, the integration of QC with quantum sensing opens up advanced applications, enhancing the precision and efficiency of data processing. Quantum sensors, utilizing the same foundational principles as QCs, provide sensitive measurements of physical phenomena. The data they generate, inherently quantum, is ideally processed by QCs, facilitating direct and efficient analysis without the need for conversion. This synergy is particularly impactful in Positioning, Navigation, and Timing (PNT) services, where quantum enhancements bring unprecedented accuracy and robustness against interference, significantly improving both civilian and military applications.

Overall, the promise of QC extends beyond sheer computational speed, offering revolutionary approaches to problem-solving and data analysis across various domains, including enhanced AI, advanced cryptography, and precision measurements.

QC represents a paradigm shift in computational capabilities, offering exponential growth in processing power over classical computing. This increase is primarily due to the principles of superposition and entanglement, which allow QCs to handle vast datasets and perform complex calculations much more efficiently than classical computers. Such capabilities open new horizons for solving problems that are currently beyond reach, including simulations that require immense computational resources and complex optimization problems in real time.

Look Before You Leap: Clarifying Misconceptions About Quantum Speed

A common misconception about QC is that it is universally faster than classical computing. QCs do not simply perform all computations faster than their classical counterparts. Instead, the strength of QC lies in its ability to handle a vastly larger computational space through superposition and entanglement. This capability allows QCs to process complex, high-dimensional problems simultaneously, which would be infeasible for classical computers. QC offers a unique advantage for specific types of issues where these properties can be fully utilized, such as large-scale optimization problems, simulations of quantum physical processes, and specific cryptographic algorithms. Therefore, the true power of QC is not just in speed but in its ability to fundamentally change the approach to complex problem-solving by exploring many possibilities in parallel. In fact, the number of gate operations needed for a given problem utilizing a certain number of qubits is generally thought of as prohibitive in the current state of computing (Iyengar, Zhang, Saha, & Ricard, 2023).

Revolutionizing Industries

The impact of QC extends across multiple sectors. In pharmaceuticals, it promises to accelerate drug discovery by simulating molecular interactions at a level of detail far beyond the capabilities of classical computers. In finance, QA can optimize portfolios and simulate economic outcomes under vast arrays of variables, offering new tools for risk management and investment strategies. Additionally, in logistics and manufacturing (Quantum Economic Development Consortium, 2024), QC could revolutionize supply chain optimization by solving complex routing problems that today’s computers cannot efficiently handle.

Enhancing Artificial Intelligence and Machine Learning

 QC also holds the potential to significantly advance the fields of artificial intelligence (AI) and machine learning, as well as quantum artificial intelligence (QAI). By processing information in fundamentally new ways, QA can train on larger datasets and execute more complex models, potentially reducing the time needed for AI systems to learn. This could lead to more accurate predictions, more sophisticated AI capabilities, and applications that we have yet to imagine.

As AI and machine learning models become increasingly complex, the power consumption required to support their computational demands on classical computing systems has escalated significantly. Training sophisticated AI models and profound learning algorithms involves massive datasets and extensive computational resources, leading to high energy costs and environmental concerns. This surge in power consumption highlights a crucial limitation of classical architectures, which struggle to balance computational efficiency with energy efficiency. QC, with its ability to perform specific calculations more efficiently than classical systems, presents a promising alternative. By potentially reducing the time and energy needed to process complex computations, QC could help make AI development more sustainable and less energy-intensive, aligning with growing demands for greener technologies.

QC can potentially help address the problem of high-power consumption in classical AI computations through several vital mechanisms:

1. Quantum Efficiency: Quantum algorithms have the potential to perform certain computations more efficiently than classical algorithms. For instance, quantum machine learning algorithms can leverage quantum parallelism and entanglement to process information in ways that dramatically reduce the number of steps required to perform calculations. This can lead to faster computations using significantly less energy than classical computers for the same tasks.
2. Handling Large Datasets: QCs can theoretically handle exponentially larger datasets than classical computers without a linear increase in energy consumption. This is particularly beneficial for machine learning models that require large-scale data processing, potentially reducing the energy required per computation.
3. Quantum Annealing: This technique is used for solving optimization problems, a common task in machine learning, such as training deep neural networks. Quantum annealers can potentially find solutions faster and more efficiently than classical optimization methods, which often require intensive computational resources and, consequently, high energy consumption.
4. Speed of Computation: QC can speed up the training phase of AI models. Faster processing times mean less time for hardware to run, which directly translates to energy savings. This is crucial for tasks like deep learning, where training models can take weeks using classical computing resources, consuming a substantial amount of electricity.
5. Reducing Carbon Footprint: By reducing the energy required for massive computations, QC could help lower the carbon footprint associated with running large data centers that are currently needed for training and operating AI systems. This aligns with the broader goal of making technology development sustainable.
6. Hybrid Quantum-Classical Approaches: In the near term, hybrid models that use both classical and QC resources could optimize energy usage by assigning tasks to the most efficient processor, whether quantum or classical. This approach maximizes the strengths of both technologies, managing power consumption more effectively while maintaining performance.

It is important to note that while QC holds significant promise, it is still in the early stages of development. Many of the advantages mentioned are theoretical or have been demonstrated only in controlled experimental settings. The full potential of QC in reducing energy consumption for AI will become more apparent as the technology matures and becomes more accessible for practical applications.

The concept of “quantum economic advantage,” as defined by the Massachusetts Institute of Technology (MIT), refers to the point at which QC not only achieves superior computational performance over classical computing for specific tasks but also does so in an economically beneficial way. (see Figure 10-6) This notion extends beyond merely performing calculations faster; it encompasses the broader economic impact, such as cost savings, efficiency gains, and enabling new types of services or products that were not previously feasible.

Quantum economic advantage suggests that QCs need to solve problems not just differently but more effectively from a financial standpoint, considering factors like cost of operation and the practicality of implementation in real-world scenarios. This is particularly important in sectors where QC could provide significant advantages over classical systems by handling complex calculations that involve large datasets or require new forms of modeling.

The research highlights several critical factors for businesses considering the adoption of QC, such as the feasibility of the QSs to handle specific tasks and whether these systems can deliver solutions more cost-effectively than traditional methods. Understanding these elements helps companies evaluate the potential return on investment in quantum technologies and determine when it might be advantageous to transition from classical to QC solutions. This framework is crucial for businesses as they navigate the evolving landscape of quantum technologies, ensuring that investments align with long-term strategic benefits and provide a clear economic advantage.​

Impact on Cryptography

One of the most talked-about impacts of QC is on the field of cryptography. QCs have the potential to break many of the cryptographic systems currently in use by exploiting algorithms like Shor’s algorithm, which can factor large numbers exponentially faster than classical algorithms. This capability necessitates the development of quantum-resistant cryptography to secure data in a post-quantum world.

As QC poses significant threats to current cryptographic methods, mainly through algorithms like Shor’s, which can break widely used encryption schemes such as RSA and ECC, the field of cryptography is evolving to address these challenges. This evolution includes the development of post-quantum cryptography (PQC), which comprises cryptographic systems that are secure against both classical and quantum attacks yet can be implemented on classical computing systems. PQC aims to create algorithms that can withstand the computational power of QCs before these devices become widely available, ensuring a smooth transition and maintaining data security.

In parallel, quantum key distribution (QKD) presents a method of secure communication that uses the principles of QM to exchange encryption keys with guaranteed security. QKD exploits the properties of QM, such as the no-cloning theorem and the observer effect, which ensures that the legitimate parties will detect any attempt at eavesdropping on the key exchange. This method allows for the creation of theoretically unbreakable keys, provided that the implementation is perfectly secure, making it an appealing option for ultra-secure communications in an era of QC (National Security Agency/Central Security Service, n.d.).

Together, post-quantum cryptography and quantum key distribution represent proactive and reactive approaches to the security challenges posed by QC. While PQC prepares our current infrastructure for a future where QCs are common, QKD uses quantum technology itself to leapfrog ahead, offering a new paradigm in secure communication.

Sensing and Data Processing

 Quantum sensing represents another cutting-edge application of QM, exploiting the extreme sensitivity of quantum states to their surrounding environments to measure physical quantities with unprecedented precision. These sensors use properties such as superposition and entanglement to detect changes in magnetic fields, gravity, time, and temperature far beyond the capabilities of classical sensors. The data generated from quantum sensors is inherently quantum, making it ideally suited for processing by QCs. This synergy allows for the direct utilization of quantum data without the need for conversion, enabling more efficient and precise data analysis. For instance, QCs can process information from quantum sensors used in deep space exploration or subatomic research, where traditional computing might struggle with the quantum nature of the data. This integration of quantum sensing with QC not only enhances the capabilities of each technology but also opens new avenues in research and technology, such as highly accurate navigation systems, advanced geological surveys, and even new methods for studying the fundamental constituents of the universe.

In the energy sector, quantum sensing and QC hold immense promise for revolutionizing traditional approaches to resource exploration, management, and optimization. Quantum sensing technologies, leveraging the principles of QM, enable overly sensitive measurements of physical phenomena such as magnetic fields, gravitational forces, and chemical compositions. These advancements in sensing technology have the potential to enhance resource discovery, improve reservoir characterization, and optimize extraction processes in oil and gas exploration, geothermal energy production, and renewable energy development. Furthermore, QC offers unprecedented computational power for analyzing vast datasets generated by energy infrastructure and operations. By harnessing quantum algorithms and processing techniques, energy companies can optimize energy distribution networks, forecast demand patterns, and optimize energy production strategies with unparalleled precision and efficiency. The integration of quantum sensing and QC technologies promises to revolutionize the energy sector, driving innovation, efficiency, and sustainability in the quest for a cleaner, more resilient energy future (Quantum Economic Development Consortium, 2023).

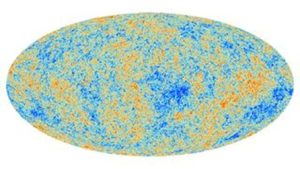
Argonne National Laboratory is leveraging quantum technologies to enhance their measurements of the cosmic microwave background (CMB), the faint afterglow light from the early universe. These measurements are crucial for understanding the universe’s origins and its composition over time. At the core of their efforts, Argonne is using advanced detection technologies, such as the South Pole Telescope’s SPT-3G camera, which is equipped with superconducting detectors that are extremely sensitive to the tiny temperature variations in the CMB. These variations help cosmologists piece together the early history of the universe, studying phenomena like gravitational lensing—a process where the mass of large objects like galaxies bends the path of the CMB light, similar to a lens bending visible light. The SPT-3G camera, due to its high number of detectors, significantly enhances the resolution and sensitivity of the observations, allowing for more detailed measurements of the CMB. These measurements are not just for academic curiosity but are crucial for validating theories about the universe’s structure and the distribution of dark matter and dark energy, which influence the universe’s expansion and large-scale structure. Argonne’s work, in collaboration with other institutions, continues to push the boundaries of what we understand about the cosmos, utilizing quantum technologies to capture and analyze data from the far reaches of space, providing insights that are critical for both theoretical physics and our understanding of the fundamental forces and particles that compose our universe. (Argonne National Laboratory, 2024)

Enhancements to Positioning, Navigation, and Timing (PNT)

Quantum technologies offer transformative improvements to Positioning, Navigation, and Timing (PNT) systems, which are vital for a wide range of applications, from military operations to civilian use in navigation systems and telecommunications. Quantum sensors, particularly those that exploit quantum entanglement and superposition, can significantly enhance the accuracy and reliability of PNT services. These sensors are less susceptible to interference and can detect beautiful changes in the environment, such as variations in gravitational fields, which classical sensors might miss. When combined with QC, the data from quantum sensors can be processed more effectively, enabling real-time calculations and adjustments that improve the precision of location and timing information. This quantum-based approach not only provides a higher level of performance but also introduces new capabilities in secure navigation and robustness against threats like jamming or spoofing, which are critical concerns in both defense and civilian sectors.

Enhancements to Critical Infrastructure

In the realm of finance, QC and quantum technologies hold immense potential to revolutionize traditional banking systems, investment strategies, and transaction processing. With their unparalleled computational power, QCs can optimize complex financial algorithms, enabling faster and more accurate risk assessment, portfolio management, and trading strategies. Moreover, quantum-enhanced encryption techniques can bolster the security of financial transactions and blockchain networks, protecting against emerging cyber threats and ensuring the integrity of digital assets. As quantum technologies continue to advance, they can enhance financial inclusion and accessibility, empowering individuals and communities to participate in global economic systems more seamlessly. By harnessing the transformative capabilities of QC and quantum technologies, the financial sector can pave the way for a more resilient, efficient, and inclusive global economy, benefiting humanity at large.

In the realm of critical infrastructure, QC and quantum technologies offer unprecedented opportunities for transformative advancements across a spectrum of sectors beyond finance. With their unparalleled computational power, QCs have the potential to revolutionize traditional systems, strategies, and operations in fields ranging from energy and transportation to communication and healthcare.

QC’s impact on energy infrastructure, for instance, could optimize resource allocation, enhance grid stability, and facilitate the development of more efficient renewable energy technologies. Similarly, in transportation, quantum algorithms could streamline logistics, optimize traffic flow, and improve the efficiency of supply chain management, leading to reduced costs and enhanced resilience.

Moreover, the application of quantum-enhanced encryption techniques holds promise for bolstering cybersecurity across critical infrastructure sectors, protecting against emerging cyber threats, and ensuring the integrity of sensitive data and communication networks. From securing transportation systems and water treatment facilities to safeguarding healthcare records and emergency services, quantum technologies offer robust solutions for protecting critical assets and infrastructure.

Furthermore, as quantum technologies continue to advance, they have the potential to enhance accessibility and inclusivity across critical infrastructure sectors, empowering individuals and communities to participate more seamlessly in global economic systems. By harnessing the transformative capabilities of QC and quantum technologies, essential sectors of infrastructure can pave the way for a more resilient, efficient, and interconnected world, benefiting humanity at large.

Summary of Computing

We have laid the foundational understanding of QC, beginning with an exploration of classical computing and its inherent limitations. We delved into the fundamental principles of QM, illustrating how they underpin the extraordinary capabilities of QCs. Through a discussion of core QC concepts such as qubits, superposition, entanglement, and quantum gates, we have seen how QCs are poised to revolutionize computing by processing information in fundamentally novel ways.

We also examined the transformative potential of QC across various sectors, highlighting its impact on artificial intelligence, machine learning, and particularly cryptography, with an emphasis on the emerging fields of post-quantum cryptography and quantum key distribution. Furthermore, the integration of QC with quantum sensing illustrated the technology’s ability to enhance the precision and efficiency of data analysis, notably in advanced applications like Positioning, Navigation, and Timing (PNT).

As we conclude this introduction, QC not only challenges our traditional understanding of computational limits but also opens a myriad of possibilities for addressing some of the most complex problems facing humanity today.

In the next section, “QC Technologies,” we will explore the various modalities of QCs, such as superconducting qubits, trapped ions, and photonic systems. This discussion will include an analysis of the advantages and challenges associated with each technology, providing a comprehensive understanding of the current state and prospects of QC hardware. As we venture deeper into the mechanisms that make QC possible, we will further appreciate the innovative strides being made toward realizing this groundbreaking technology’s full potential.

Quantum Technologies

QC represents a groundbreaking shift in our approach to data processing, challenging the very fundamentals of classical computing with its radically different mechanism of action. Unlike classical computers, which operate using bits as the basic unit of information, QCs use quantum bits, or qubits, which can exist in multiple states simultaneously. This ability to hold and process a vast array of possibilities in a single quantum state is what potentially allows QCs to perform complex calculations at unprecedented computational size and, thus, computational speeds.

The diversity in QC technologies—often referred to as modalities—stems from the various physical systems that can effectively represent and manipulate qubits. Each modality leverages different aspects of QM to achieve this, ranging from the superposition and entanglement of particles to the use of photons or trapped ions. The choice of modality impacts not only the potential power and speed of a QC but also its reliability, scalability, and the nature of problems it can effectively solve.

Developing QC technologies faces significant material challenges that often stem from the quantum nature of the devices themselves. These challenges include:

• Material Purity and Quality: High levels of material purity are crucial for minimizing quantum decoherence, a phenomenon where quantum information is lost due to interactions with the environment. Even microscopic impurities or defects can significantly affect the performance of quantum devices.
• Temperature Sensitivity: Many QSs, such as superconducting qubits, require extremely low temperatures to function. Maintaining such conditions is not only challenging but also energy-intensive and expensive.
• Fabrication Complexity: Creating and manipulating quantum devices often requires precise and complex fabrication processes that can be difficult to scale. This is particularly true for technologies like trapped ions and photonic qubits, where aligning and integrating components with the required precision is technically demanding.
• Material Innovation: The advancement of QC technologies is heavily reliant on breakthroughs in material science. Researchers continually seek new materials and methods to control quantum states better and improve the coherence times of qubits.

These material challenges highlight the intersection of QC with other fields of scientific research, such as materials science and engineering. Addressing these issues is crucial for the development of practical and scalable QCs, as each technological hurdle overcome brings us a step closer to realizing the full potential of QC.

Superconducting Qubits

Superconducting qubits represent the most promising and extensive research modalities in QC. These quits leverage the properties of superconducting materials, which can conduct electricity without resistance at extremely low temperatures, to perform quantum computations. This type of qubit is made from circuits containing elements like capacitors and Josephson junctions – the latter being the critical component that exploits the quantum mechanical phenomenon of tunneling. In these circuits, the flow of Cooper pairs (pairs of electrons bound together at low temperatures) creates a quantum state that can be controlled and read electronically. This setup allows the qubits to operate in a coherent quantum state long enough to perform calculations, making them a strong candidate for building scalable QCs. [1]

As a quantum mechanical phenomenon in chemistry and physics where certain materials can conduct electricity without resistance when cooled below a characteristic critical temperature, this remarkable property results in the complete disappearance of electrical resistance, which is a stark contrast to the behavior of ordinary conductive materials where electrical resistance causes energy dissipation as heat. Critical Temperature (Tc) is the temperature below which a material becomes superconductive. The necessary temperature varies widely among superconductors, ranging from near absolute zero (-273.15°C) up to higher temperatures of around -135°C in some newer compounds. Superconductivity arises when two electrons with opposite spins pair up through a quantum mechanical effect facilitated by lattice vibrations in the material’s crystal structure. These pairs, known as Cooper pairs, can move through the lattice without scattering, which is what typically causes resistance in conventional conductors. One of the defining characteristics of superconductivity is the Meissner effect, where a superconducting material will expel all magnetic fields from its interior when it transitions into the superconducting state. This effect demonstrates the perfect diamagnetism of superconductors, meaning they will repel a magnetic field perfectly.

Types of Superconductors

There are two primary types of superconductors: Type I and II.

Type I Superconductors

These materials have a single critical magnetic field, beyond which superconductivity is destroyed. They are typically pure elemental metals.

Type II Superconductors

These materials have two critical magnetic fields, between which they can exist in a mixed state of normal and superconducting regions. Type II superconductors are often used in high magnetic field applications due to their ability to maintain superconductivity under higher magnetic fields.

Applications of Superconductivity

Superconductivity remains an area of intense research, with scientists striving to develop materials that can achieve superconductivity at higher temperatures, potentially revolutionizing energy transmission and various other technologies by drastically reducing energy losses. Superconductors have a wide range of applications due to their unique properties:

Magnetic Levitation

It is used in applications like maglev trains, where powerful superconducting magnets allow the train to float above the tracks, reducing friction and allowing for very high speeds.

Medical Imaging

Superconducting materials are crucial for MRI machines, which use superconducting magnets to generate significant and stable magnetic fields necessary for high-resolution imaging.

Particle Accelerators

Superconducting materials are used in the electromagnets of particle accelerators to maintain the high currents needed without the significant energy losses seen in regular conductors.

QC

Superconductors provide the basis for superconducting qubits, which are used to build quantum circuits that operate with high efficiency due to the absence of electrical resistance.

Fabrication of Superconducting Qubits

The fabrication of superconducting qubits heavily relies on techniques borrowed from the semiconductor industry. These qubits are typically created on silicon or sapphire substrates using advanced lithographic methods similar to those used in the manufacture of traditional semiconductor devices. The process involves the deposition of superconducting materials such as aluminum or niobium onto the substrate, followed by precision patterning and etching to create the microscopic circuits that form the qubits.

The semiconductor industry, critical to the development of superconducting qubits, also brings with it a range of human and ethical challenges that are amplified in the high-stakes realm of QC. One primary concern is the environmental impact associated with semiconductor manufacturing, which often involves toxic chemicals and significant water and energy consumption. The push toward advancing QC technologies must consider these ecological costs, striving for sustainable practices that reduce harm to ecosystems and human health.

Furthermore, the geopolitical implications of semiconductor manufacturing cannot be overlooked. As countries vie for technological superiority, especially in strategic areas like QC, the concentration of manufacturing capabilities in certain regions raises issues of supply chain security and economic dependence. These dynamics pose ethical questions regarding access to technology and the potential for global inequities in the benefits derived from quantum advancements.

Additionally, there is the challenge of workforce development and safety. The highly specialized nature of QC and semiconductor manufacturing requires skilled workers who often face high-pressure environments and exposure to hazardous materials. Ensuring fair labor practices and worker safety is paramount, necessitating rigorous regulatory standards and ethical oversight.

By addressing these human and ethical considerations, the QC sector can contribute to a more equitable and sustainable technological future, aligning the incredible potential of quantum advancements with the broader goals of societal well-being and environmental stewardship.

Superconducting qubits are particularly appealing due to their fast gate speeds and relatively straightforward integration into existing electronic technology. Their manufacturing process benefits from decades of innovation in semiconductor fabrication, allowing for the use of established infrastructure and expertise to scale up quantum devices.

Despite their advantages, superconducting qubits face significant challenges. They require extremely low operational temperatures (close to absolute zero), which demands sophisticated and costly cooling systems. Additionally, these qubits are susceptible to various types of noise and decoherence, which can interfere with their performance. Researchers are continually working to improve the coherence times and stability of these qubits through better materials, design modifications, and isolation techniques.

Significant research and development efforts are ongoing to enhance the viability of superconducting qubits. Innovations in materials science, such as the development of new superconducting compounds or the improvement of Josephson junctions, are critical areas of focus. Furthermore, advancements in cryogenic technology and quantum error correction methods are essential for addressing the operational challenges of these QSs.

The deployment of cryogenic technology in QC raises ethical and social issues related to access and equity. The high cost of cryogenic systems may limit the availability of QC technology to well-funded institutions and wealthy nations, potentially widening the technology gap between developed and developing countries. This disparity could influence who benefits from the scientific, medical, and technological advancements enabled by QC.

The integration of cryogenics into QC also affects industries by requiring specialized equipment and expertise, thus creating new market opportunities and economic activities. These include the development of advanced cryogenic systems and the materials needed for them, which can drive job creation and economic growth in high-tech sectors. The operation of cryogenic systems, especially in the context of QC, involves high energy consumption, mainly due to the need to maintain temperatures close to absolute zero. This requirement can contribute to increased energy demand and carbon emissions, posing challenges for sustainability. However, advancements in energy-efficient cryogenic technology and the potential environmental benefits of QC-driven innovations (such as more efficient chemical processes and materials science advancements) could mitigate these impacts.

Trapped Ions

Trapped ion technology is one of the leading approaches in the field of QC. This modality leverages the unique properties of ions—atoms that have been electrically charged by adding or removing electrons—to perform quantum computations.

In chemistry, an ion is defined as an atom or molecule that has gained or lost one or more of its electrons, resulting in a net electric charge. Unlike neutral atoms, which have equal numbers of electrons and protons, ions have an imbalance between the number of protons (positively charged particles) and electrons (negatively charged particles), which gives them either a positive or negative charge. Types of Ions:

1. Cations: These are positively charged ions that have more protons than electrons. Cations are formed when an atom loses electrons. This loss typically occurs because the atom’s outermost electrons are not firmly bound to the nucleus, making them relatively easy to remove. Common examples of cations include sodium (Na+), which loses one electron, and calcium (Ca2+), which loses two electrons.
2. Anions: These are negatively charged ions that have fewer protons than electrons. Anions form when an atom gains electrons. The addition of electrons usually happens when the atom has a robust electronegative pull that attracts electrons to fill a valence shell. Examples of anions include chloride (Cl^-), which gains one electron, and sulfate (SO4^2-), which gains two electrons.

Ions play crucial roles in various chemical processes:

• Chemical Bonding: Ions are fundamental to the formation of ionic bonds, where positively charged cations and negatively charged anions attract each other to form ionic compounds, such as sodium chloride (table salt).
• Electrolytes: In solutions, ions conduct electricity and are essential for the function of electrolytes in biological organisms. They help regulate nerve and muscle functions and maintain fluid balance.
• Redox Reactions: Ions participate in oxidation-reduction (redox) reactions, which are vital for processes such as metabolism, photosynthesis, and cellular respiration.

Understanding the behavior of ions is essential in fields ranging from biochemistry and environmental science to industrial processes and materials science.

Trapped ions are manipulated in an ultra-high vacuum environment where they are confined using electromagnetic fields. These ions act as qubits, the fundamental units of quantum information. Lasers are used to initialize, manipulate, and read the quantum state of these ions, allowing for the execution of quantum gates and algorithms. The ions’ ability to maintain coherence over relatively long periods and their high fidelity in quantum operations make them strong candidates for scalable QC. One of the most significant advantages of trapped ion technology is the high degree of control over the qubits, which leads to meager error rates in quantum operations. Additionally, ions can be individually addressed and entangled with a high degree of precision using laser beams, facilitating complex quantum computations. The long coherence times of trapped ions allow for prolonged manipulation and interaction, which are crucial for executing intricate quantum algorithms.

Despite their advantages, trapped ion systems face several challenges. The technology requires sophisticated apparatus to trap and cool the ions, often involving elaborate setups with lasers, vacuum chambers, and magnetic traps. Scaling up trapped ion systems to handle a large number of qubits remains a technical challenge, as each additional qubit increases the complexity of the system. Moreover, the operational speed of quantum gates in trapped ion systems is generally slower compared to other technologies like superconducting qubits, posing a limitation for certain types of quantum computations.

Ongoing research in trapped ion technology focuses on overcoming scalability and operational speed limitations. Innovations such as the development of microfabricated ion traps and integrated photonics are being explored to make these systems more compact and efficient. Leading research groups and companies are continually advancing the technology, aiming to build more robust and scalable QCs based on trapped ions.

Trapped ions utilize individual ions as qubits. Each ion can be precisely controlled and manipulated to represent quantum states. Typically, the qubits are encoded in the electronic states of the ions, which can be selectively excited using lasers. For example, different energy levels of an ion’s electrons might represent the binary states 0 and 1, or more complex configurations can be used to represent superpositions of these states.

The quantum state of each ion qubit can be initialized into a specific state using a combination of optical pumping and laser cooling techniques. Measurement of the qubit’s state is performed by using a method known as state-dependent fluorescence, where the ion emits light at specific frequencies depending on its quantum state, which can then be detected and interpreted.

Quantum logic gates, which are essential for quantum computation, are implemented in trapped ion systems by applying sequences of laser pulses. These pulses precisely control the interactions between the qubits, allowing for the execution of complex quantum algorithms. The qubits can be entangled through their mutual Coulomb interactions mediated by laser-induced forces, a critical feature for performing quantum computations.

Manufacturing Trapped Ions Qubits 

The process of creating and utilizing trapped ions for QC involves sophisticated techniques and relies on a variety of industries and infrastructures. Trapped ions are typically manufactured from atoms that are ionized—meaning electrons are removed to create positively charged ions. This ionization is commonly achieved through laser ablation or electron bombardment, processes where a target material is struck with a high-energy laser pulse or electrons to dislodge electrons from atoms.

Once ionized, the ions need to be trapped and controlled. This is done using devices known as ion traps, which use electric or magnetic fields to confine ions in a small region of space. The most common types of ion traps used in QC are:

• Paul Traps: This uses oscillating electric fields to trap ions. The traps are designed to confine ions dynamically, allowing them to be held in stable conditions for extended periods.
• Penning Traps: These utilize a combination of static electric and magnetic fields to confine ions. They are handy for holding large numbers of ions.

Trapped ions must be cooled to very low temperatures to minimize their kinetic energy, which helps in precise control and manipulation. Laser cooling is the primary technique used, where the absorption and emission of photons slow down the motion of ions.

In the context of trapped ion QC, cryogenics is not typically a central requirement for the operation or manufacture of trapped ion systems. Unlike certain other QC technologies, such as superconducting qubits, which require extremely low temperatures close to absolute zero to maintain superconductivity and reduce noise, trapped ion systems generally operate at or near room temperature.

While cryogenics is not fundamentally necessary for trapped ion QC, it can still play a role in specific advanced experimental setups, particularly in enhancing the system’s performance:

1. Reducing Background Collisions: Cooling the environment around trapped ions can help reduce background gas collisions, thus potentially extending the coherence times of the ions. Lower temperatures lead to fewer air molecules being present that could interact with the ions, which reduces decoherence.
2. Minimizing Thermal Noise: In some specific trapped ion experiments, particularly those involving very high precision measurements or quantum simulations, cryogenic environments may be used to reduce thermal noise. This enhances the precision of quantum state manipulations and measurements.
3. Enhanced Control Over Ions: Some research has explored the use of cryogenically cooled ion traps to achieve better control over the ions. Cooling the trap itself, rather than the ions directly, can lead to more stable trapping potentials and reduced electric noise from the trap electrodes.

Most trapped ion systems rely on other sophisticated technologies such as:

• Ultra-high Vacuum Systems: To prevent the ions from interacting with air molecules, which could lead to energy loss or decoherence, trapped ions are maintained in an ultra-high vacuum.
• Laser Systems: Used for ionization, cooling, and manipulation of the ions. Lasers allow for precise control of ion quantum states, crucial for performing quantum operations.
• Magnetic and Electric Field Generators: These create the fields necessary to trap and manipulate ions in spatial configurations for quantum computations and interactions.

Advantages of Using Trapped Ions as Qubits 

Trapped ion systems offer several compelling advantages as a platform for qubits, each contributing to their potential as a cornerstone of QC technology. Known for their high fidelity, trapped ions allow for quantum operations to be performed with meager error rates, a crucial attribute for the reliability and accuracy of quantum computations. Additionally, ions are capable of maintaining their quantum states—or coherence—for relatively long periods, an essential quality for executing complex and lengthy quantum computations without information loss.

A distinct advantage of using trapped ions is their addressability; each ion can be independently manipulated with precision using lasers. This ability is not only critical for the implementation of error correction protocols but also for the scalability of QC systems. Recent technological advancements have further enhanced this scalability through the development of modular systems. In these systems, ions housed in separate traps can be interconnected via photonic links, allowing for the expansion of the QS while maintaining the high level of control and fidelity that trapped ions are known for. This combination of individual power and potential for interconnectivity makes trapped ions an up-and-coming candidate for advancing QC into a more scalable and practical phase.

Trapped ion systems offer several compelling advantages as a platform for qubits, each contributing to their potential as a cornerstone of QC technology. Known for their high fidelity, trapped ions allow for quantum operations to be performed with meager error rates, a crucial attribute for the reliability and accuracy of quantum computations. Additionally, ions can maintain their quantum states—or coherence—for relatively long periods, an essential quality for executing complex and lengthy quantum computations without information loss.

A distinct advantage of using trapped ions is their addressability; each ion can be independently manipulated with precision using lasers. This ability is not only critical for the implementation of error correction protocols but also for the scalability of QC systems. Recent technological advancements have further enhanced this scalability through the development of modular systems. In these systems, ions housed in separate traps can be interconnected via photonic links, allowing for the expansion of the QS while maintaining the high level of control and fidelity that trapped ions are known for. This combination of individual power and potential for interconnectivity makes trapped ions an up-and-coming candidate for advancing QC into a more scalable and practical phase.

Fundamental Operations with Trapped Ions

1. Qubit Representation: Trapped ions utilize individual ions as qubits. Each ion can be precisely controlled and manipulated to represent quantum states. Typically, the qubits are encoded in the electronic states of the ions, which can be selectively excited using lasers. For example, different energy levels of an ion’s electrons might represent the binary states 0 and 1, or more complex configurations can be used to represent superpositions of these states.
2. Initialization and Measurement: The quantum state of each ion (qubit) can be initialized into a specific state using a combination of optical pumping and laser cooling techniques. Measurement of the qubit’s state is performed by using a method known as state-dependent fluorescence, where the ion emits light at specific frequencies depending on its quantum state, which can then be detected and interpreted.
3. Quantum Manipulation and Gate Operations: Quantum logic gates, which are essential for quantum computation, are implemented in trapped ion systems by applying sequences of laser pulses. These pulses precisely control the interactions between the qubits, allowing for the execution of complex quantum algorithms. The qubits can be entangled through their mutual Coulomb interactions mediated by laser-induced forces, a critical feature for performing quantum computations.

Trapped ion technology has significant potential in the field of space exploration. Ion propulsion systems, which utilize ions accelerated by electric fields to create thrust, are an example of how this technology can be employed in space missions. These systems offer a highly efficient form of propulsion, providing a higher specific impulse compared to traditional chemical rockets. Furthermore, trapped ion QC could be used on spacecraft for complex computational tasks that require robustness against harsh space conditions, such as radiation and extreme temperatures. The ability to process data directly onboard spacecraft with QCs could significantly enhance mission capabilities and speed up space exploration.

In the context of PNT, trapped ion systems could revolutionize how we understand and utilize quantum sensors. Quantum sensors based on trapped ions offer unprecedented accuracy in timekeeping and navigation systems. This high precision is crucial for applications like global positioning systems (GPS) and other navigation technologies that rely on exact timing to function accurately. The superior stability and sensitivity of trapped ion clocks can help reduce errors in GPS measurements, leading to more reliable and precise navigation capabilities, which are essential not just for civilian use but also for military operations.

In medicine, the precise control and measurement capabilities of trapped ion technology can be utilized in imaging and diagnostic tools. For instance, ion traps can be used in mass spectrometry for susceptible detection of molecules, which is crucial in identifying trace amounts of chemicals in biological samples. This can enhance capabilities in everything from drug discovery to the early diagnosis of diseases by detecting biomarkers that are present only in deficient concentrations. Additionally, the advanced computational power of trapped ion QCs might one day assist in modeling complex biological systems, potentially accelerating personalized medicine and the design of new therapeutics.

While trapped ion technology offers various benefits, it also raises ethical and social considerations. The deployment of advanced PNT and medical diagnostic tools must be handled responsibly to ensure privacy and data protection, especially in tracking and health monitoring contexts. Additionally, as with all advanced technologies, there is a need to ensure equitable access to the benefits brought by trapped ion innovations. Addressing these ethical considerations is crucial to ensure that advancements in trapped ion technology contribute positively to society and do not exacerbate existing inequalities.

Photonic Systems

Photonic systems utilize photons, the fundamental particles of light, as the medium for quantum computation. Unlike electrons or ions, photons are massless and can travel at the speed of light, making them ideal for high-speed quantum communications and computing. In photonic QC, information is encoded in the quantum states of photons, such as their polarization, phase, or path.

Quantum properties of light arise from its dual nature, where it exhibits both wave-like and particle-like behaviors. In QM, light is described not just as electromagnetic waves but also as discrete packets of energy called photons. Here are the critical quantum properties of light that are fundamental to understanding phenomena in quantum physics and technology, including QC:

1. Particle-Wave Duality:

Particle Aspect: Light can be thought of as consisting of particles or photons, each carrying a quantum of energy. The particle nature of light is evident in phenomena such as the photoelectric effect, where light can knock electrons off a metal surface, suggesting that light interacts with matter as discrete particles.

Wave Aspect: Light also exhibits wave-like properties, such as interference and diffraction, which are characteristic behaviors of waves. This duality is central to many quantum experiments and technologies.

2. Quantization of Energy: Photons are quantized in energy, meaning that a photon’s energy is proportional to its frequency. This relationship is described by the equation E = hf, where E is energy, ℎ is Planck’s constant, and f is the frequency of the light. This quantization is crucial in phenomena like the photoelectric effect and in technologies that rely on specific photon energies, such as lasers.
3. Superposition: Photons can exist in a superposition of states, a fundamental principle of QM. For a photon, this could mean being in multiple polarization states or paths simultaneously. Superposition allows for complex quantum interference effects and is exploited in QC and quantum cryptography.
4. Entanglement: Photons can become entangled, meaning the quantum state of one photon is related to the state of another, regardless of the distance separating them. This entanglement is a powerful resource for QC and quantum communication, enabling phenomena like quantum teleportation and quantum key distribution.
5. Polarization: Polarization is a quantum property that describes the orientation of the light waves’ oscillations. Photons can be polarized in various directions, and QSs use these states to encode information. Quantum cryptography often uses the polarization states of photons to secure information transmission.
6. No-Cloning Theorem: In QM, the no-cloning theorem states that it is impossible to create an identical copy of an arbitrary unknown quantum state. This property is critical for quantum communication, as it means that any attempt to eavesdrop on quantum-encoded messages cannot go undetected.
7. Heisenberg Uncertainty Principle: For photons, the Heisenberg Uncertainty Principle implies that specific pairs of physical properties, like position and momentum or energy and time, cannot both be precisely measured or known simultaneously. This principle is essential for understanding the limits of measurement and control in quantum optics.

These quantum properties make light uniquely suitable for a range of applications in quantum technologies, from computing and simulations to secure communications and sensing. Each property opens different possibilities and challenges in harnessing light for advanced technological applications.

Photonic qubits utilize photons, the fundamental particles of light, as the carriers of quantum information. These qubits are manipulated using optical components such as beam splitters, phase shifters, and detectors. One of the critical advantages of photonic qubits is their inherent resistance to decoherence, as photons are less prone to environmental noise compared to other physical systems. This property makes photonic systems promising candidates for building large-scale QCs with high-fidelity operations. In photonic QC, quantum gates are implemented using optical elements to perform operations on photonic qubits. For example, beam splitters and phase shifters can be used to perform single-qubit operations. At the same time, nonlinear optical processes such as parametric down-conversion can enable the generation of entangled photon pairs for implementing two-qubit gates. These gate operations allow for the execution of quantum algorithms and computations using photonic qubits.

Photonic QC offers several advantages, including high-speed operation, low error rates, and compatibility with existing fiber optic communication networks. Additionally, photons can be easily manipulated and detected using optical components, enabling the realization of complex quantum circuits. However, challenges remain in the generation, manipulation, and detection of photonic qubits with high efficiency and scalability. Overcoming these challenges is crucial for the practical realization of photonic QCs for various applications. Photonic QC holds promise for a wide range of applications, including quantum cryptography, quantum simulation, and quantum machine learning. For example, photonic QCs could be used to simulate complex QSs, optimize financial portfolios, or solve optimization problems in logistics and supply chain management. With ongoing advancements in photonics and quantum technologies, the future of photonic QC appears bright, paving the way for transformative breakthroughs in science, technology, and society.

Future Perspectives

QC is not limited to the well-known types such as superconducting qubits, trapped ions, and photonic systems. Several emerging modalities are also showing promise due to the unique advantages they offer in quantum processing capabilities.

Topological qubits represent an advanced approach to QC, which relies on manipulating the topological states of matter. These qubits harness quasiparticles called anyons, whose world lines cross over one another to form braids in a two-dimensional space, creating robust quantum states that are highly resistant to local noise and decoherence. The main benefit of topological qubits lies in their inherent error resistance. The errors in quantum calculations typically arise from environmental disturbances, but the topological nature of these qubits protects the quantum information, potentially reducing the need for complex error correction protocols. The primary challenge is the actual realization and manipulation of anyons, as they require particular conditions to exist, such as at extremely low temperatures and in unique materials. (Leon & et al., 2021)

Silicon quantum dots use small silicon structures to confine electrons or holes in a way that their quantum properties can be harnessed for computing. These quantum dots are similar in design to traditional semiconductor devices, which could allow them to be more easily integrated with existing silicon-based electronic technology. Compatibility with existing semiconductor manufacturing techniques is a significant advantage, potentially allowing for more effortless scalability and integration with classical computing infrastructure. Silicon is also characterized by having naturally long coherence times, which is essential for QC. Precise control over the quantum dot size, position, and electron occupancy remains challenging, along with ensuring uniformity across a large-scale QS.

Looking ahead, the field of QC is poised for exciting advancements as these additional modalities continue to develop. Future QCs might integrate multiple modalities to leverage the strengths of each. For example, photonic systems could be used for quantum communication between quantum processors that use superconducting qubits or silicon quantum dots. Advances in material science are crucial for all quantum modalities, but especially for topological qubits and silicon quantum dots. Discovering new materials or improving the quality of existing ones could significantly enhance the performance and feasibility of these QSs. As modalities like topological qubits inherently reduce error rates, they could simplify the overall architecture of QCs and reduce the overhead required for error correction, a significant hurdle in current QC designs. Each modality faces its own set of scalability challenges, but breakthroughs in fabrication, control technologies, and quantum error correction could lead to more commercially viable QCs. The eventual goal is to produce a QC that can outperform classical computers in a wide range of applications, achieving what is known as quantum supremacy. As these technologies advance, they will also raise important regulatory and ethical issues that must be addressed, including data security, privacy, and the implications of potentially disruptive technologies.

Algorithms and Applications

QC represents a monumental shift in our ability to solve complex problems, heralding a new era of computational capability with profound implications for humanity. At the heart of this revolution are quantum algorithms, which leverage the enigmatic properties of QM—such as superposition, entanglement, and quantum interference—to perform tasks that are intractable for classical computers. From optimizing logistical operations to developing life-saving drugs and securing sensitive communications, quantum algorithms have the potential to address some of the most pressing challenges facing society today. This section explores innovative algorithms like Shor’s for integer factorization and Grover’s for database searching, delving into their mechanisms and discussing their broad applications across various industries. By harnessing these powerful tools, QC is not just enhancing our technological capabilities but is poised to deliver substantial benefits to humanity, driving forward sectors such as finance, healthcare, materials science, and beyond.

In the realm of computational science, specific problems are notoriously difficult to solve, not merely due to their complexity but because of their fundamental nature. These problems, often classified as NP-hard, push the limits of classical computing, presenting challenges that are not just computationally intensive but may also be practically unsolvable as problem sizes increase. QC leverages unique algorithms designed to take advantage of QM principles, such as superposition, entanglement, and interference. These algorithms offer significant computational advantages for certain types of problems.

NP-hard problems, such as TSP or optimizing molecular structures considering the Pauli Exclusion Principle, do not currently have efficient solutions in classical computing and are expected to benefit from quantum computational approaches. QCs can potentially exploit their inherent properties like entanglement and superposition to navigate the vast computational landscapes of these problems more efficiently than classical systems.

National Aeronautics and Space Administration (NASA) defines NP-hard problems as aligning with the standard definition in computational complexity theory. An NP-hard problem is a type of problem that is at least as hard as the most complex problems in the NP class. This means that any problem in NP can be reduced to an NP-hard problem in polynomial time. In simpler terms, if you can find a way to solve the NP-hard problem efficiently, you can theoretically solve all problems in the NP class efficiently using that solution. NASA often encounters NP-hard problems in various computational and engineering challenges, such as optimizing mission trajectories, scheduling communications with spacecraft, and solving other logistical and engineering problems that are critical to space exploration. The classification of a problem as NP-hard indicates that it is expected to be challenging to solve and that there may not be a polynomial time solution available, which is a crucial consideration when planning and executing missions that require complex and reliable computational support. Understanding and identifying NP-hard problems helps NASA and other organizations anticipate the computational challenges and allocate resources effectively, possibly using heuristic or approximation methods to obtain good enough solutions in practical time frames where exact solutions are not feasible due to computational constraints. (R.Biswas & et.al, 2017)

SHOR’s Algorithm

This is perhaps the most famous quantum algorithm, developed by Peter Shor in 1994. It provides an efficient method for factoring large integers, an essential process in cryptography. Shor’s algorithm can factor numbers exponentially faster than the best-known classical algorithms, which poses a threat to current cryptographic systems based on the difficulty of factoring large products of prime numbers.

GROVER’s Algorithm

Developed by Lov Grover in 1996, this algorithm offers a quadratic speedup for unstructured search problems over classical counterparts. For example, suppose you have a list of unsorted items. In that case, Grover’s algorithm can find a specific item in roughly the square root of the number of items significantly faster than the linear time required by classical algorithms.

Quantum Fourier Transform (QFT)

The QFT is a quantum equivalent of the discrete Fourier transform and is a critical component of many quantum algorithms, including Shor’s algorithm. It transforms a quantum superposition of integer states into another superposition according to their Fourier coefficients, facilitating the extraction of periodicities from quantum states.

The Traveling Salesman Problem (TSP)

One of the most famous NP-hard problems is the Traveling Salesman Problem (TSP). The TSP asks whether, given a list of cities and the distances between each pair of cities, there is a round-trip route that visits each city exactly once and returns to the origin city, minimizing the total distance traveled. Classical algorithms struggle to solve the TSP efficiently because the number of possible routes increases factorially with the number of towns, making exhaustive searches impractical for even moderately sized datasets.

QC offers new potential for tackling the TSP through quantum optimization algorithms, which can explore multiple possibilities simultaneously thanks to quantum superposition. For example, quantum annealing and variants of Grover’s algorithm are investigated for their potential to find optimal solutions more efficiently than classical approaches, thereby reducing the solution space exploration time dramatically.

Variational Quantum Eigensolver (VQE)

Variational Quantum Eigensolver (VQE) is a quantum algorithm. It is designed to find the eigenvalues of a Hamiltonian, which is especially useful in quantum chemistry and material science problems. VQE is particularly notable for its hybrid approach, combining quantum and classical computing techniques, which makes it well-suited for implementation on current noisy intermediate-scale quantum computers. VQE utilizes both quantum and classical resources. The quantum part of the algorithm prepares quantum states and measures the expectation value of the Hamiltonian corresponding to these states. The classical part involves optimization techniques that adjust the parameters of the quantum state to minimize the energy expectation value. VQE can potentially offer significant computational advantages over traditional classical computational methods, particularly for problems where classical computations become infeasible due to the exponential growth of the Hilbert space with the number of particles. It is primarily used to simulate molecular systems and materials. It provides a way to study the properties of molecules, including ground state energy, excited states, and reaction mechanisms, which are crucial for drug discovery, material design, and understanding fundamental chemical processes.

Conclusions

Understanding and solving the complex problems that our society faces have profound implications across various sectors. For instance, optimizing molecular simulations can revolutionize drug discovery by finding new compounds efficiently or enhance materials science by predicting new materials’ properties before they are synthesized. Similarly, solving logistical problems like the TSP can significantly optimize operations in sectors ranging from transportation to supply chain management. QC holds transformative potential for numerous industries that form the backbone of infrastructure, such as power, communications, transportation, and healthcare, to name a few:

• Energy Systems Optimization: In the energy sector, QC can optimize grid management and the integration of renewable sources, potentially revolutionizing how we distribute and conserve energy. This optimization includes more efficient routing of electricity to reduce losses and enhance the predictability of renewable outputs.
• Transportation and Logistics: Quantum algorithms can significantly improve route planning and logistics, reducing costs and environmental impact for global shipping and local delivery services. These improvements are critical as transportation networks become more complex and heavily integrated.
• Communications Networks: QC enhances the security and efficiency of communication networks, mainly through the development of quantum encryption techniques such as quantum key distribution, which can safeguard data against emerging cyber threats.
• Public Safety and Emergency Services: By enabling faster and more accurate simulations and data analyses, QC can improve prediction models for natural disasters, enhance emergency response strategies, and potentially save lives by providing earlier warnings and more effective resource allocation.

Beyond enhancing physical infrastructures, QC also addresses broad societal challenges. Healthcare advancements using QC accelerate biomedical research and the development of new treatments by simulating biological processes that would be infeasible to model on classical computers. This capability can lead to breakthroughs in understanding complex diseases and developing new drugs. The technology also offers the potential to model complex environmental systems accurately, aiding in climate research and the development of more effective environmental protection strategies. This can help mitigate the impacts of climate change and manage natural resources more sustainably. In the realm of security, quantum technologies provide potent tools for encryption and secure communications. Still, they also necessitate new defensive measures against quantum-enabled cyber threats, reshaping global cybersecurity landscapes. As quantum technologies advance, they raise critical questions about accessibility and the equitable distribution of their benefits. Ensuring that QC developments benefit humanity broadly requires careful policy and ethical considerations, particularly in making sure these technologies do not exacerbate social inequalities. QC pushes the boundaries of what is scientifically possible, facilitating significant advancements in various fields of research and industry. This progress could redefine technological limits, from how we generate power to how we explore space.

As we stand at the cusp of a new era marked by the advent of QC, the revolutionary changes it brings are not just technological but profoundly transformative for society as a whole. QC, with its promise to solve complex problems that have long eluded classical systems, holds the potential to redefine industries, enhance our understanding of the natural world, and address some of the most pressing challenges facing humanity today. For those who have witnessed the rise of digital technology from its infancy, the emergence of QC might recall the early days of computers and the internet. Just as those technologies transformed the world in ways that were hard to imagine at their inception, so too does QC stand poise to open new horizons. This transition offers an opportunity for us to reflect on our past advancements and inspire us to shape a future that leverages this powerful new tool responsibly and effectively. For the older generation, embracing QC is not merely about adapting to new technologies but about contributing to a legacy of innovation and wisdom that will benefit future generations. It is an invitation to participate in shaping a future where technology continues to catalyze positive change—improving healthcare, protecting the environment, and enhancing global security.

As we navigate this new quantum frontier, the role of ethical stewardship becomes paramount. The decisions we make today about how to develop and deploy QC technology will have long-lasting implications. It is essential to approach these decisions with a commitment to fairness, equity, and sustainability, ensuring that the benefits of QC are shared broadly and contribute to the betterment of all. There is also a significant opportunity to pass on knowledge and inspire younger generations to explore the possibilities inherent in QC. By supporting education and opportunities for young people to engage in this exciting field, the older generation can help cultivate the next wave of scientists, engineers, and thinkers who will continue pushing the boundaries of what is possible. QC represents a profound shift in our ability to understand and manipulate the fundamental building blocks of the universe. As we look to the future, let us draw on the wisdom accrued from past experiences to guide us. Let us engage with this new technology not just as passive observers but as active participants, contributing our insights and values to ensure that as the quantum age dawns, it leads to a brighter, more equitable, and more sustainable world for all.

The advancement of the frontier of quantum technologies is imperative to comprehensively educate our scientists and engineers in the intricacies of QM and QC cannot be overstated. Without a robust and detailed understanding of these complex fields, there is a genuine risk that the implementation of such technologies, especially within our critical infrastructures, could be vulnerable to manipulation or misapplication. This vulnerability could leave our systems open to strategic deception by adversaries, ultimately jeopardizing not just individual components but our entire societal framework. It is, therefore, critical that we invest in thorough and rigorous training for our future quantum workforce, ensuring they are equipped with the knowledge necessary to implement these powerful technologies securely and effectively. This approach will not only protect but also fortify our infrastructure against potential threats, preserving the integrity and resilience of our societal functions.

The actual watershed moment in the evolution of quantum computing lies in its potential to solve NP-hard problems, which have long stood as colossal challenges in computational sciences. The ability of QC to address these complex problems could revolutionize numerous fields, from cryptography and logistics to drug discovery and artificial intelligence. This breakthrough signifies more than just an advancement in computing power; it represents a paradigm shift in how we approach and solve the most intricate and computationally intensive problems known today. As we continue to refine and harness this technology, the solutions to previously intractable challenges could not only enhance our technological capabilities but also dramatically expand the horizons of human knowledge and problem-solving abilities. The promise of quantum computing in transforming our approach to NP-hard problems is not just a leap forward; it is a leap into a new realm of possibilities that redefines the boundaries of innovation and human ingenuity.

References

Argonne National Laboratory. (2024, 5 21). Cosmic microwave background. Retrieved from anl.gov: https://www.anl.gov/cmb

ATLAS Collaboration. (2012). Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physics Letters B, 1-29.

BBC NEWS. (2013, 12 28). Cosmic Microwave Background Radiation As Measured By Quantum Sensing. Retrieved from https://www.bbc.com: https://www.bbc.com/news/science-environment-23691292

Description Of Qubit As A Bloch Sphere And Related Quantities That Describe The States It Can Form. (2024, 5 21). Retrieved from Wikimedia: https://commons.wikimedia.org/wiki/File:Bloch_sphere.svg

Iyengar, S. S., Zhang, J. H., Saha, D., & Ricard, T. C. (2023). Graph‐|Q⟩⟨C|: A Quantum Algorithm with Reduced Quantum Circuit Depth for Electron Structure. The Journal of Physical Chemistry, 9334-9345.

Khan, A., Sharkey, K. L., & & Chancé, A. (2022, May). quantum-chemistry-and-computing-for-the-curious/. Retrieved from https://www.packtpub.com: https://www.packtpub.com/product/quantum-chemistry-and-computing-for-the-curious/9781803243900

Leon, N. P., & et al. (2021, 4 16). Materials challenges and opportunities for quantum computing hardware. Retrieved from https://www.science.org/doi/10.1126/science.abb2823: https://www.science.org/doi/10.1126/science.abb2823

Levine, I. N. (2014). Quantum Chemistry. Boston: Pearson.

MIT Sloan Office of Communication. (2023, 11 17). https://mitsloan.mit.edu/press/will-quantum-computing-be-better-your-business. Retrieved from https://mitsloan.mit.edu/press/will-quantum-computing-be-better-your-business: https://mitsloan.mit.edu/press/will-quantum-computing-be-better-your-business

National Security Agency/Central Security Service. (n.d.). Cyber Security. Retrieved from National Security Agency: https://www.nsa.gov/Cybersecurity/Quantum-Key-Distribution-QKD-and-Quantum-Cryptography-QC/

Quantum Economic Development Consortium. (2024, March 19). Publications. Retrieved from Quantum Computing for Transportation and Logistics: https://quantumconsortium.org/transportation-logistics/

Quantum Economic Development Consortium. (2023, September 8). Publications. Retrieved from Quantum Economic Development Consortium: https://quantumconsortium.org/quenergy23/

R.Biswas, & et.al. (2017, 5 Volume 64, May 2017, Pages 81-98). A NASA perspective on quantum computing: Opportunities and challenges. Retrieved from https://www.sciencedirect.com/science/: https://www.sciencedirect.com/science/article/abs/pii/S0167819116301326

Sharkey, K. L. (n.d.). AI-Generated Image Of Computer Scientist Contemplating The Quantum Realm. Book 9 Figure 10.1. London.

Sharkey, K. L. (n.d.). AI Rendering Of Alien Space Craft In Rotational Option In A Cosmological Space. Book 9. London.

Sharkey, K. L. (n.d.). AI Rendering Of Futurist Origami-Based Spacecraft With Astronaut Aboard Hovering In A Solar System Above Some Landscape. Book 9 Figure 2. London.

Sharkey, K. L. (n.d.). AI Rendering Of Interconnected Computing Technologies. Book 9. London.

Zare, R. (1991). Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics. Wiley.

End Notes:

[1]  The chapter author has written /published extensively on the generalized Qubit-Cooper Pair equations. Derivations of these functions are beyond the scope of this chapter. However, readers may consult her available books and papers on the subject.

[2] Figure 10-1: Source: (Sharkey, AI-Generated Image Of Computer Scientist Contemplating The Quantum Realm.)

[3] Figure 10-2: Sources: (Quote Author Unknown; Sharkey, AI Rendering Of Futurist Origami-Based Spacecraft With Astronaut Aboard Hovering In A Solar System Above Some Landscape)

[4] Figure 10-5: (Source: Description Of Qubit As A Bloch Sphere And Related Quantities That Describe The States It Can Form., 2024)