9 Chapter 9: Chinese Advances in Stealth UAV Penetration Path Planning in Combat Environment [Nichols]

Student Objectives

The task of planning a flyable, safe, paths for stealth UAVs to penetrate the US or allied forces Air Defense Systems (ADS) is considered.  Students will gain a fundamental knowledge of path planning in terms of computer modelling of the path objective functions and cost of paths from node to node in a network. Constraints of collision avoidance, maneuverability, control, torsion, 2D /3D, communications,  kinematics, SCADA are interwoven in the coverage of modeling goals. Special emphasis will be on the advances reported by Chinese researchers in improving the standard path planning models by including model-based predictive control and multi-step search methodology to increase the threat effectiveness for penetrating an ADS using stealth UAVs.

Introduction

In our previous books on UAS and CUAS, the authors covered a huge range of topics: UAVS, threats, vulnerabilities, countermeasures, radar, IFF, DEW, AI, autonomy, advanced systems technology, stealth design, safe flight activity in the NAS, legal and regulatory considerations, cyber taxonomies, INFOSEC, INFOWAR,  SCADA, SWARMS, acoustical defenses, US ADS, ADS-B, GPS spoofing, Chinese New Silk Road Land and Sea Strategic advances, and more. (Nichols R. K., et al., 2019)(Nichols R. K., et al., 2020)

The authors were concerned with the Counter- UAS Problem (see below). (Nichols R. K., et al., 2020) Essentially, the authors were reactive in dealing with hostile UAS penetration of US ADS networks. What the authors did not cover was the path planning for a stealth UAV in static or dynamic civilian or combat environment. This chapter explores some of computer models and methodology to plan strategic UAV penetrations into a host civilian or combat complex environment.

The treatment is cursory as our students do not need to be aviation engineers or Red / Blue team members. They do need to be familiar with the behind the scenes technology. This chapter starts off with the C-UAS problem and attack on the Abqaiq Oil Facilities by Houthi terrorists. It then morphs into questions of how the Houthis ’succeeded where they had failed in the past; what the Chinese technology addition did for them; how this attack could be modelled / enacted with advanced UAV path planning techniques; and what elements are common to the modelling of such dynamic environment for UAS / UAV penetration.

What Is the Counter -UAS Problem?

The risk of successful terrorist attacks on USA Air Defense Systems (ADS) via sUAS/UASs is greater because of improving commercial capabilities and accessibility. Advanced small drones, capable of carrying sophisticated imaging equipment and significant payloads, are readily available to the public.  A range of terrorist, insurgent, criminal, corporate, and activist threat groups have demonstrated their ability to use civilian drones and gather intelligence. How does the (or any)  country defend against a growing UAS threat? This is also known as the counter – UAS Problem. General James D Mattis, SECDEF summed up the Problem succinctly: (Nichols R. K., et al., 2019)

“Unmanned Aircraft are being developed with more technologically systems and capabilities. They can duplicate some of the capabilities of manned aircraft for both surveillance/ reconnaissance and attack missions. They can be small enough and / or slow enough to elude detection by standard early warning sensor systems and could pose a formidable threat to friendly forces.” (Chairman, 2012) The Saudi Arabian government has incorporated / purchased many of the US and Israeli ADS technologies into its own ADS.

Implications from Attack by Iran on Saudi Arabian Oil Fields

On 14 September 2019, Houthi rebels in Yemen claimed their attack on the Abqaiq and Khurais oilfields in Saudi Arabia. (Gallagher, 2019) The effect was to temporarily take out 5% of the global oil production capacity. (Gallagher, 2019) Houthi rebels claimed responsibility for the attack, saying that 10 drones (mixed origins) and 17 missiles were deployed. (Lister, 2019)  Ballistic missile attacks by the Houthis have been previously deployed using old Soviet and Iranian “Scud” SRBMs. No prior attack, since the Yemen conflict began four years ago, has interrupted oil supplies.

The Houthis have sent dozens of drones and short-range ballistic missiles against Saudi Arabia in the past two years. Many have been intercepted by Saudi Air Defenses; others have fallen harmlessly. Very few have caused limited damage and casualties. (Lister, 2019) The Abqaiq oilfield is 800 miles from Houthi-held parts of Yemen. The drones used were from North Korean  Iranian and Chinese technology origins. (Lister, 2019) The Iranian drones were dubbed the UAV-X and have a range of 740 – 930 miles. This is a step up from the SRBMs that were based on North Korean technology with a maximum range of  186 miles. (Lister, 2019) The Chinese drones have several names: “Qaseth-1” (“Striker-1”), a rebrand of the Iranian Ababil-2 UAV and the “Mirsad-1” used by Hezbollah until 2018. (Gallagher, 2019) The step-up in the conflict game is the Iranian clone, KH-55 with a range of 1,550 miles. These were reportedly used in the Saudi Arabian oil field attacks. (Gallagher, 2019) The Iranian clone uses Chinese path planning stealth penetration technologies.[1]

The take-away from this attack is not just the loss of global oil processing capacity and H2S stabilization processing facilities[2] but the vulnerability and exposure of the Saudi Arabian Advanced Air defenses. Most of the Saudi Arabian ADS are designed to defend against traditional threats and are ill-equipped to tackle the asymmetrical aerial threats such as drones.  The vulnerability is enhanced when so many essential oil-related infrastructure parts are concentrated in a small area: storage, processing, compressor trains and distribution. (Lister, 2019) Threats and vulnerabilities of US ADS were covered in (Nichols R. K., et al., 2020) and apply to the ADS used by Saudi Arabia (SA) Over the last two decades, SA has purchased many of their ADS from both US and Israel.

Think of this problem more globally. China, North Korea, and Iran [referred to as CNKI technology cooperation] are aggressively cooperating on drone technologies for use by terrorists against a major oil production region. The technology is cost-effective as well as human capital efficient. Drones substituting for manned aircraft. Drones penetrating the SA ADS.

Figure 9-1 Shows A haze of smoke is seen from the attacked oil plant in Saudi Arabia

Source: (Sheena McKenzie, 2019)  https://www.cnn.com/middleeast/live-news/saudi-oil-attack-dle-intl/h_1ab7e8469e98525f887c3a4e588dde8a

Let us expand the threat. Refer to Figure 9-2. Note that the Strait of Hormuz lies between Iran and Saudi Arabia, with Bahrain, Qatar, UAE, and Oman in the sandwich. Between the Gulf of Oran and the Persian Gulf, about 20% of the global oil movement / supply travels through the Strait of Hormuz. (EIA, 2019) The US 5th Fleet currently protects this oil flow. There have been several clashes between Iranian vessels and US Vessels. Drones cross over the US Fleet every day and test its patience.

Remember, payloads can be anything: CBRN deployment devices, drugs, surveillance packages, shaped charges, lasers, super resolution cameras, weather instruments, GPS/GNSS cyber weapons, missiles, etc.

The problem is twofold: what is the risk assessment for CNKI drone technologies cooperation acted on either target (US 5th Fleet or Saudi Oilfields -both in range of  KH-55’s) and what countermeasure technologies are available to counter the threats presented and to mitigate those risks and system vulnerabilities? Previous works have covered the topics of conventional countermeasures against SUAS / UAS and  aggressor counter-countermeasures specific to UAS deployment – SWARMS. (Nichols R. K., et al., 2020)

Figure 9-2 Strait of Hormuz

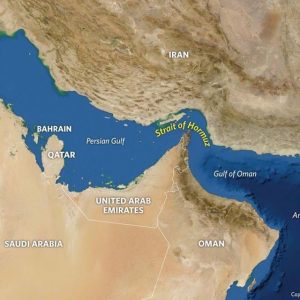
Source: (Stratfor, 2019)

What else did the Chinese give the Terrorists besides the advanced KH-55 Missiles and Drones?

The answer is they taught the terrorists how to use the drones more effectively by showing them how to computer model and plan the penetration paths for their stealth UAVs in a combat environment.

Chinese Advances in Rapid Path Planning for Stealth UAV in Complex Environment with Bandit Threats

In a recent paper slated for publication in the International Journal of Aerospace Engineering, Drs Zhang, Wu, Dai, and He, presented computer modeling results from their research into the subject of low altitude combat. Their paper addresses “a novel algorithm for stealth UAV to realize the rapid penetration path planning, which aims to devise a penetration strategy based on the improved A-Star algorithm to address problems of path planning and planning (sic) for stealth UAV in the complex dynamic environment. The proposed method introduces the kinematic model of stealth UAV and detection performance of netted radar in the process of low altitude penetration. Combined with the prediction technique and path planning algorithm, the multi-step search strategy is developed for stealth UAV to deal with POP-UP [3]threats and complete the planning  (sic)of the path in different scenarios. Furthermore, the attitude angle information is integrated into the improved A-Star algorithm, which reflects the characteristics of the dynamic radar cross-section(RCS) and conforms to the actual flight requirements for the stealth UAV. Finally, the improved A-Star algorithm, learning real-time A-Star algorithm(LRTA-Star), and dynamic A-Star algorithm(D-Star) are respectively adopted to settle the problem of penetration path planning for stealth UAV in three different threat scenarios. Numerical simulations are performed to illustrate that the proposed approach can achieve rapid penetration path planning for stealth UAV indifferent dynamic threat scenarios and verify the validity of the improved A-Star algorithm.”  (Zhang, 2020)

Novelty

The Zhang paper presents a novel addition to the A-Star algorithm for path planning in a dynamic combat environment with “POP-UP” / Bandit threats. The novelty is an upgrade from the standard EW training on radar systems and Air Defense Systems (ADS). (Adamy D. -0., 2015) (Skolnik, 2008) The optimization techniques and computer algorithms (in present day computer programming languages) have been well researched and are not novel. (Reklaitis G. R., 1983) (Horowitz, 1978)

What is novel about the authors’ paper is the real time dynamics and predictive control applied to stealth UAV path planning via computer modelling. It results in a computationally multi-step search pattern. The non-exclusive but mathematically necessary goals of flyable paths, collision avoidance, computational efficiency and reduced RCS are ably met with the authors’ improved A Star algorithm. This gives us an insight into how far ahead the Chinese may be in the field.

Keep in mind that UAVs at low altitude rarely have IFF capability due to SCADA constraints and that Counter UAS (CUAS) technologies can bypass stealth features in combat and civilian UAVs. (Nichols R. K., et al., 2020) (Nichols R. K., et al., 2019) The validity of the algorithm is demonstrated in known mathematical bounded datasets with cases for  single, dual, and networked radar surveillance systems. No real flight data is used. To many students in UAS, the above material is like jumping out of plane without a parachute.

UAV Path Planning

Time to take a stroll down cooperative path planning for UAVs in various environments. Then maybe we can recycle back to the Zhang paper with just enough knowledge to get a sense of the novelty of the technology about to be published by the Chinese researchers. The clearest reference on the subject of Path Planning of UAVs is by Tsourdos, White and Shanmugavel. (Tsourdos, 2011) We will draw heavily from this fundamental textbook. [4] There are other fine textbooks on this subject to enhance the student knowledge: (Angelov, 2012), (Austin, 2010), (Barnhart, 2012), and (Dalamagkidis, 2012)

Path planning is a complex problem, which involves meeting the physical constraints of UAVs, constraints from the operating environment and operational requirements. Paths must be flyable. Flyable paths meet kinematic constraints of the UAV. Satisfaction of this constraint means that the motion of the UAV stays within bounds on maneuver curvature. Paths must exhibit CA for threats, obstacles, and other UAVs. Minimum fuel, energy conservation,  and shortest distance come into play for an efficient and better performance path. (Tsourdos, 2011) Path planning algorithms produce one or more safe flyable paths for the UAVs. Path length, limited range, survey area, and flying direction all make a difference. The UAV trajectory must comply with speed and maneuver constraints; deployment of several UAVs in a coordinated manner which involve CA and simultaneous arrival at one or more locations. Lastly the algorithm that optimizes all these conditions must be computationally efficient, work in real-time, re-plan its trajectory if needed and with no significant delay. (Tsourdos, 2011)[5]

Path Planning Formulation

The primary aim of path planning is to provide structured mobility and to facilitate moving or flying multiple UAVs from one location to another. Several locations may mean several paths before reaching the final destination. On any known or partially known map /area there may be several points of interest (POIs).[6] The UAV has a specific attitude, which combined with its location to give the UAV pose[7] P(x, y, z, θ, Ψ), where x, y, z, is the UAV location or waypoint and (θ, Ψ) are the horizontal and vertical angles , respectively. (Tsourdos, 2011)

Consider a UAV moving from one starting pose, Ps to another, finish Pf . Path planning involves producing one or more flight paths r(q) connecting Ps and Pf  represented as

                                                    r(q)

Ps ————>Pf                                                           (9.1)

Where r(q) is the resulting path, and q is defined as a path parameter. This parameter can be a lengths variable (0 < q < s) for a straight-line path or an angle variable (0 < q > θ). The choice of the path variable depends on the path formulation.

Equation (9.1) is re-written  for a single UAV as:

                                                          r(q)

 Ps (xs, ys, zs, θs, Ψs) ————>Pf (xf, yf, zf, θf, Ψf)                     (9.2)

Extending for N UAVs, where each pair of poses are connected by paths ri (q):

                                                                        ri(q)

Ps (xsi, ysi, zsi, θsi, Ψsi) ————>Pf (xfi, yfi, zfi, θfi, Ψfi)                     (9.3)

Where I =1,…..,N.

Equation (9.3) connects a pair of points by a path. This also represents route planning for one or more nodes of a network. The UAV route is usually defined by a set of waypoints joined by straight-line segments.  However, these may not be flyable because UAVs cannot turn instantaneously through each waypoint. This is why waypoints require orientation for each segment to match – essentially a common tangent to produce a continuous path. (Tsourdos, 2011)Thus, some segments might be curved or curvy-linear to meet the common tangent condition. SAA sensors for ISTAR missions must be pointed in specific directions for effective detection and identification. (Nichols, et al., Counter Unmanned Aircraft Systems Technologies and Operations, 2020)

Path Planning Constraints

Various constraints are involved in path planning.  There are two general types: UAV-specific and those arising from obstacles in the environment. (Tsourdos, 2011) Violation of these constraints (i.e. communication failure) may lead to the complete loss of the UAV or sensor platform. Safety is a consideration for the mission.  Turn radius also dictates which paths are flyable.

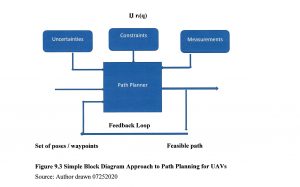
Figure 9.3 Simple Block Diagram Approach to Path Planning for UAVs

Source: Author drawn 07252020

Turn radius also dictates which paths are flyable. Paths must balance safety and flyability. Flyable paths meet kinematic  or motion constraints  and dictate maneuverability of the UAVs. (Tsourdos, 2011) Let Џ represent constraints. So (9.3) is written to include constraints (9.4). We now have enough information for a simple Black Box representation, Figure 9.1.

The inputs to Figure 9.1 are the poses, with additional constraints, uncertainties, and measurements. The feedback loop senses the measured states of the UAV and feeds back the success in terms of meeting the constraints to the path planner. (Tsourdos, 2011)

                                                                      Џ ri(q)

Psi (xsi, ysi, zsi, θsi, Ψsi) ————>  Pfi (xfi, yfi, zfi, θfi, Ψfi)                     (9.4)

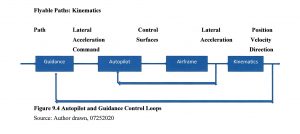
Figure 9.4 Autopilot and Guidance Control Loops

Source: Author drawn, 07252020

Paths need to meet the dynamic constraints of the UAV . They are influenced by the motion of the UAV. Essentially we have a SCADA control system. (Nichols R. K., et al., 2019) Refer to Figure (9.2) which shows autopilot and guidance control loops.

The inner feedback loop is the autopilot and the outer feedback loop is the guidance system. The guidance system provides lateral acceleration commands to keep the UAV on path. The autopilot controls the UAV elevator, ailerons, and rudder to achieve the required lateral acceleration. (Tsourdos, 2011)

UAV dynamics include the aerodynamics, which produces forces and torques on the airframe. (Durham, 2013) Newton’s third law of motion dictates that forces and torques produce lateral, longitudinal, and rotational accelerations. The accelerations are usually expressed in UAV body axes and these provide the link to kinematics. (Tsourdos, 2011) Kinematics is produced by integrating the UAV lateral and rotational acceleration vectors to obtain the UAV velocity vector.  The attitude angles and current UAV position in the inertial frame give the UAV’s translational and rotational velocity. The 2D path planner uses the kinematic model in equation (9.5a-b):

ẋ = / v / cos (θ)                                                 (9.5a)

ẏ = / v / sin (θ)                                                  (9.5b)

where v is the UAV velocity and (θ) is the horizontal heading angle. (Tsourdos, 2011)

Whether a given path is flyable is determined by the curvature of the path. The path planning algorithm has to produce a path r(q) that meets the dynamic turn rate constraint of the UAV, which is translated into the kinematic curvature constraint in 3D. It is determined by both the curvature and torsion. (Lipschutz, 1969) The curvature at any point on the path must be less than the maximum-curvature constraint of the UAV because it is proportional to the lateral acceleration. (Lipschutz, 1969) A curve segment of zero curvature is just a straight line and a curve segment of a constant curvature is an arc of a circle. At any given speed, v, the lateral acceleration a is proportional to the curvature k such that:

/ a / = / v2 / k ∞ k                                        (9.6)

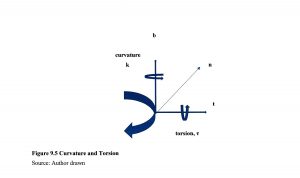
                                                  Figure 9.5 Curvature and Torsion

Source: Author drawn

Where a is the lateral acceleration vector, k is the curvature, v is the velocity vector and ∞ is a vector operator. For a constant speed, the acceleration vector a is normal to the velocity vector v. This ensures that the velocity vector rotates without changing its magnitude. Refer to Figure 9.3where the velocity vector is aligned with the tangent vector t and the acceleration vector is aligned with the normal vector n. (Tsourdos, 2011)

Maneuver Coordinates

All maneuvers ca that coincide with the path tangent vector. n be defined by reference to a set of coordinates. 2D path planning confines the maneuvers to a plane.  If the plane is horizontal, this is equivalent to flying at a constant altitude. In 3D space, flyable paths need to accommodate both curvature and torsion in their design. Curvature defines the turn radius of the path in 2D, which is defined as a rotation about an axis normal to the maneuver. Torsion is defined as a rotation about an axes. See Figure 9.3 Note that positive curvature and positive torsion are defined as being clockwise along the appropriate axis viewed from the origin. For a UAV, in terms of body axes, curvature is equivalent to yaw rate turn and torsion is equivalent to a roll rate turn. In practice, UAVs will perform the turn by rolling to a fixed bank angle and then using the elevator to produce a maneuver normal to the wings. [8] (Tsourdos, 2011)

Generation of Safe Paths

The second important constraint of path planning is safety. Safety is measured by the ability of a UAV to avoid fixed and moving obstacles, and other AC or UAVs. Safety is represented in terms of a constraint that maintains flyability and collision avoidance. It is represented by Џsafe and is used to modify path planning equation (9.4). Џk considers the curvature constraint:

                                           Џsafe Џk ri(q)

Ps (xsi, ysi, zsi, θsi, Ψsi) ————>Pf (xfi, yfi, zfi, θfi, Ψfi)                     (9.7)

Other constraints could be added to the above equation. For example, communication constraint on UAV separation distance could be represented by Џcomm.  (Tsourdos, 2011)

Collision Avoidance (CA)

Collision avoidance between two flight paths r1(q) and r2 (q) can be represented by:

             r1(q) ∩  r2 (q) = 0                                                                     (9.8)

This equation captures the condition required to be satisfied for CA. A cooperative path planning of multiple UAVs for CA can be formulated as producing flight paths {r1(q), r2(q),….,rn(q)} subject to the following constraints:

Џ =  Џk,     k  ≤  kmax; and  Џτ,   τ  ≤  τmax; and Џsafe   ri(q) ∩  rj (q) = 0            i ≠ j

Such problems are solved by optimization algorithms which involves heavy computation. In many cases the problem is broken down into phases / stages. (Tsourdos, 2011) Here we have our first intersection with the Chinese improvements on the A star algorithm for path planning. (Zhang, 2020)

A huge amount of work had been done in optimization algorithms to solve UAV and other problems. The best reference on the subject is Reklaitis. (Reklaitis G. R., 1983) Of interest to the reader are three optimization path finding algorithms: A-Star, D-Star, and improved A-Star with predictive control. Focus will be on what makes them different / useful for UAV path planning rather the details of the algorithms which can be found in Zhang. (Zhang, 2020)

A-Star Algorithm

The A-Star algorithm is a heuristic search algorithm, which is widely performed to various agents in the path planning problems to various agents. The main thrust of the A-Star algorithm is as follows. First, select the appropriate heuristic function, estimate the generation value of the extensible search points in the target search area, comprehensively. Compare the different cost values of each point. Consider the operation time and distance cost of the track point search. Last, find an optimal path. (Wikipedia, 2020) A-Star selects the path that minimizes:

f(n) = g(n) + h(n)                                                  (9.9)

where: h(n) is the heuristic function, the estimated distance from next node n on the path to the goal node; and g(n) is the cost of the path from start node n to the goal. F(n) is the path cost function.

At each iteration of its main loop, A-Star needs to determine which of its paths to extend. It does so based on cost of the path and an estimate of cost required to extend the path all the way to the goal. (Wikipedia, 2020)

A-Star has some disadvantages: A) only the position information of the stealth UAV can be obtained in the path, and the dynamic RCS characteristics and attitude information of the stealth UAV cannot be obtained; B) unknown path cost estimation cannot be accurately calculated in path planning, the final path cannot guarantee to be globally optimal[9]; and C) performance improvements include search validity, real-time performance in face of unknown threats and the expansion of track modes. (Zhang, 2020)

D-Star Algorithm

D-Star algorithm is a variation of the A-Star algorithm suitable for solving path planning problems in unknown environments. The main idea of the algorithm is to search the reverse path from goal to the origin when a new obstacle is found in the path. The path between the target location and the path node within the range of the new obstacle will not change due to the appearance of the new obstacle, but the path between the UAV and the node within the range of the obstacle will change during flight. The whole path is only partially re-planned. The heuristic expression for the D-Star algorithm is given by:

f(X, E) = h(X) + g(X, E)                                              (9.10)

where: h(X) represents the actual journey cost from goal to state X and g(X,E) represents the estimated journey cost from the state X to the current position of the stealth UAV. (Zhang, 2020)

Chinese Improved LRTA-STAR Algorithm

Zhang describes the learning real-time A-Star algorithm (LRTA-STAR) as a heuristic search algorithm which satisfies the requirements of real-time planning in a dynamic environment by establishing and updating the evaluation cost from each state to the target point. However, the flight path planned by the single step search is composed of a series of broken lines. The maneuverability of the UAV is limited so that there is some difficulty to achieve accurate flight path tracking control. Search results are prone to traps in local dead loops, leading to failure of path planning. Zhang’s team overcame these issues by combining LRTA-STAR with two big improvements: 1) model-based predictive control (MPC) and 2) multi-step optimal search method. (MSSM) Zhang’s team extensively compared all the variations and the improved LRTA- STAR algorithm performed exceedingly well in a simulated combat scenario using stealth UAVs! Clearly they are thinking about penetration of allied ADS, something the military should take note of if not already.

MPC

Model-based predictive control is an optimization control method, which includes model prediction, rolling optimization, and feedback correction.  MPC is described in detail by Zhang. (Zhang, 2020) MPC optimal control law for a multi-step prediction is given by:

         N                                              W

J = ∑ qi [ yp (k+i) – yr (k+i)]2  +  ∑ δj [u(k+j-1)]2                                                 (9.11)

         i=1                                             j=1

where: N = length of the prediction domain; W is the length of the control domain; qi is the output prediction error, and δj is the weighting coefficient of the control variable. (Zhang, 2020)

Multi-Step Search Method (MSSM)

MSSM is a further refinement on the LTRA-STAR algorithm. It is novel search strategy based on multi-step optimization to achieve re-planning for a stealth UAV in a dynamic environment. In MSSM, the track cost of each predicted track is considered as a cumulative value of N predicted track nodes. The objective function of UAV flight planning can be obtained according to the optimal control law of the MPC system. The cost of the predicted flight path in N steps from the kth node is given by: (Zhang, 2020)

         k+N                                                                     k+w

J(k)  = ∑  [ b1T (j/k) B1b1 (j/k) +    εj Pnet  (j/k)  +  ∑ δj uT  (j/k) u (j/k)          (9.12)

           j=k                                                                       j=k

Conclusions

This chapter has touched on a premier concern of ADS systems – path planning for stealth UAVs in a combat or civilian environment. Chinese researchers appear to have a novel approach to penetrating US ADS systems with stealth UAVs.[10] Their “improved LRTA-STAR algorithm presents a new solution for path re-planning control of stealth UAV in complex network radar environments with Bandit threats.

The improved A-STAR algorithm is based on a multi-step search strategy designed by model-based predictive control and LTRA-STAR algorithm. The attitude angle information of the stealth UAV is added to the calculations. This demonstrates the variation characteristics of dynamic RCS. [11] Kinematic analysis of the stealth UAV and detection performance analysis of netted radar, the original paths and the re-planning paths can satisfy the actual flight requirements. (Zhang, 2020)

Discussion Questions

How would you implement the Chinese improved A-STAR algorithm in onboard UAV computers? The calculations are computer  / storage intensive. Could part of them be done by ground stations and the intermediate results be communicated up to the UAV in real-time? How about on missiles? Rockets? A really helpful reference on this question is by Dr Tewari. (Tewari, 2011)

References

Adamy, D. -0. (2015). EW 104 EW against a New Generation of Threats. Boston: Artech House.

Adamy, D. (2001). EW 101 A First Course in Electronic Warfare. Boston, MA: Artech House.

Adamy, D. (2009). EW 103 Tactical Battlefield Communications Electronic Warfare. Boston, MA: Artech House.

Adamy, D. (2015). EW Against a New Generation of Threats. Boston: Artech House.

Adamy, D. L. (2004). EW 102 A Second Course in Electronic Warfare. Boston: Artech House.

Adamy, D.-9. (1998, Jan). Lesson 4: the basic link for all EW functions. (electronic warfare)(EW Reference & Source Guide). Journal of Electronic Defense, Jan 1998 Issue.

Alford, L. (2000). Cyber Warfare: Protecting Military Systems. Acquisition Review Quarterly.

Angelov, P. (2012). Sense and avoid in UAS research and applications. Hoboken: NJ.

Army, U. (1992, November 23). US Army Field Manual FM 34-40-7. Communications Jamming Handbook.

Austin, R. (2010). “Design for Stealth”, Unmanned Aircraft Systems UAVS Design Development and Deployment. New York: John Wiley and Sons.

Barnhart, R. K. (2012). Introduction to Unmanned Aircraft Systems. New York: CRC Press.

Beaudoin, L. e. (2011). Potential Threats of UAS Swarms and the Countermeasures Need. ECIW.

Dalamagkidis, K. V. (2012). On Integrating Unmanned Aircraft into the National Airspace System, 2nd edition. Denver, CO: Springer.

DoD-01. (2018). JP 1-02. Retrieved from Department of Defense Dictionary of Military and Associated Terms: www.dtic.mil/doctrine/new_pubs/jp1_02.pdf

DoD-02. (2018). Information Operations (IO) in the United States. Retrieved from JP 3-13 : http://www.dtic.mil/doctrine/new_pubs/jp3_13.pdf

DoD-03. (2015). Unmanned Systems Roadmap 2013 to 2038. Retrieved from DTIC: http://www.dtic.mil/dtic/tr/fulltext/u2/a592015.pdf

DTRA. (2019, October 18). Private Communication re Aviation Vulnerabilities. (Nichols, Interviewer) Retrieved from https://www.dtra.mil/

Durham, W. (2013). Aircraft Flight Dynamics and Control. The Atrtium, Chesterton, UK: Wiley.

EIA. (2019, June 20). The Strait of Hormuz is the world’s most important oil transit chokepoint. Retrieved from EIA – US Energy Information Administration: https://www.eia.gov/todayinenergy/detail.php?id=39932

Eshel, T. (2019, September 14). AFRL to Test a Drone-Swarm Killer HPM. Retrieved from Defense Update: https://defense-update.com/20190923_hpm.html

FAA. (2018, February 1). Part 107 Rule for sUAS. Retrieved from Fly under the Special Rule for Model Aircraft: https://www.faa.gov/uas/getting_started/model_aircraft/

Filbert, F. &. (2014, (July – August). Joint Counter Low, Slow, Small Unmanned Aircraft Systems Test. Fires PB644-14, no 4. Washington: DoD.

Fitts, R. (1980). The Strategy of Electromagnetic Conflict. Los Altos, CA: Peninsula Publishing.

Gallagher, S. (2019, September 16). Missiles and drones that hit Saudi oil fields: Made in Iran, but fired by whom? Retrieved from Arstechnica.com: https://arstechnica.com/tech-policy/2019/09/missiles-and-drones-that-hit-saudi-oil-fields-made-in-iran-but-fired-by-whom/

Hartman, K. a. (2013). The Vulnerability of UAVs to Cyber Attacks – An Approach to the Risk Assessment. 2013 5th International Conference on Cyber Conflict . Tallin: NATO CCD COE Publications.

Horowitz, E. (1978). Fundamentals of Computer Algorithms. Potomac, MD: Computer Science Press.

Howard, C. (2019, June 21). What is the Strait of Hormuz, where Iran shot down US Navy drone? Retrieved from Fox News: https://www.foxnews.com/world/whats-the-strait-of-hormuz-iran-shot-us-navy-drone

Kania, E. (2017, July 6). Swarms at War: Chinese Advances in Swarm Intelligence. China Brief Volume: 17 Issue 9. China Brief Volume: 17 Issue 9.

Kaye, T. a. (2001, September 30). ACHIEVING INFORMATION DOMINANCE:. Retrieved from DODCCRP-Space and Naval Warfare Systems Center San Diego: http://www.dodccrp.org/events/2002_CCRTS/Tracks/pdf/026.PDF

Kim, A. G. (2012, June). Cyber Attack Vulnerabilities Analysis for Unmanned Aerial Vehicles. Retrieved from Infotech@Aerospace.com: https://www.researchgate.net/publication/268571174_Cyber_Attack_Vulnerabilities_Analysis_for_Unmanned_Aerial_Vehicles

Lipschutz, M. (1969). Schaums Outline for Differential Geometry. NYC: McGraw-Hill .

Lister, T. (2019, September 16). Attack is a game-changer in Gulf confrontation. Retrieved from CNN: https://www.cnn.com/middleeast/live-news/saudi-oil-attack-dle-intl/h_3e647100fa720927c962d7643472b12d

Marshall, D. M. (2016). Introduction to Unmanned Aircraft Systems, 2nd Edition. New York: CRC Press.

Moir, I. a. (2006). Military Avionics Systems. New York: Wiley Aerospace Series.

Monahan, K. (2004). The Radar Book: Effective Navigation and Collision Avoidance. Anacortes, WA: Fineedge Publications.

Myer, G. (2013, May-June). Danger Close Definition. Retrieved from US Army Magazine: www.benning.army.mil/infantry/magazine/issues/2013/May-June/Myer.html

N/A. (2020, July 25). Cambridge Dictionary on line. Retrieved from dictionary.cambridge.org/us/: https://dictionary.cambridge.org/us/

NASA. (2018). Unmanned Aircraft Systems (UAS) Integration in the National Airspace System (NAS) Project. Retrieved from NASA: https://www.nasa.gov/feature/autonomous-systems

Nichols, R. K. (2008, September 05). Counterintelligence & Sensitive Compartmented Information Facility . (SCIF) Needs – Talking Points.

Nichols, R. K. (2019, March 14). Hardening US Unmanned Systems Against Enemy Counter Measures. 7th Annual Unmanned Systems Summit. Alaxandria, VA, USA: PPTX presentation , self.

Nichols, R. K., Mumm, H. C., Lonstein, W. D., Ryan, J. J., Carter, C. M., & & Hood, J. P. (2020). Counter Unmanned Aircraft Systems Technologies & Operations. Manhattan, KS: New Prairie Press #31.

Nichols, R. K., Mumm, H. C., Lonstein, W. D., Ryan, J. J., Carter, C., & and Hood, J.-P. (2019). Unmanned Aircraft Systems in the Cyber Domain, 2nd Edition. Manhattan, KS: NPP eBooks. 27. Retrieved from www.newprairiepress.org/ebooks/27

Nichols, R. (Nov 28-30, 2006). Cyber Terrorism, Critical Infrastructure, & SCADA Presentation. In R. Nichols (Ed.), Defense Threat Reduction Agency Conference. Shirlington VA: Utica College, Utica NY.

Nichols, R., Ryan, J., Mumm, H., Carter, C., Lonstein, W., & Hood, &. J. (2020). Counter Unmanned Aircraft Systems Technologies and Operations. Manhattan, KS: New Prarie Press #31.

Nichols, R., Ryan, J., Mumm, H., Lonstein, W., Carter, C., & & Hood, J. (2019). Unmanned Aircraft Systems (UAS) in Cyber Domain: Protecting USA’s Advanced Air Assets, 2nd Edition. Manhattan, KS: New Prairie Press #27 .

Nichols, R.-0. (2016, March 29). NCIE UAS SAA Final Rev 4. 2016 INFOWARCON conference presentation April 4-7, Nichols, R.K. et. al. (3-29-2016) Presentation to INFOWARCON April 4-7 on NCIE UAS SAA Final Rev 4, presented to 2016 INFOWARCON conference, Memphis TN. Available as PPTx presentation download from author or in CANVAS. Memphis, TN, USA: INFOWARCON16.

Nielsen, P. E. (2012). Effects of Directed Energy Weapons. Middletown, DE: CreateSpace Independent Publishing Platform.

Osborn, K. (2019, October 15). Swarm Hell: Can the U.S. Army Stop Hundreds of Drones Armed with Explosives? Retrieved from National Interest: https://nationalinterest.org/blog/buzz/swarm-hell-can-us-army-stop-hundreds-drones-armed-explosives-88206

Randall K. Nichols, D. J. (2000). Defending Your Digital Assets against Hackers, Crackers, Spies and Thieves. New York: RSA Press.

Rani, C. M. (2015). Security of unmanned aerial vehicle systems against cyber-physical attacks. The Journal of Defense Modeling and Simulation: Applications, Methodology, Technology.

Reklaitis, G. R. (1983). Engineering Optimization: Methods and Practices. Boston: Wiley.

Reklaitis, G. R. (1983). Engineering Optimization: Methods and Practices. Boston: Wiley.

Sheena McKenzie, M. W. (2019, September 17). Saudi attacks send oil prices soaring. Retrieved from CNN: https://www.cnn.com/middleeast/live-news/saudi-oil-attack-dle-intl/h_1ab7e8469e98525f887c3a4e588dde8a

Singer, P. W. (2010, February 25). Will Foreign Drones One Day attack the US? . Newsweek.

Skolnik, M. (2008). Radar Handbook, 3rd Edition. Boston: McGraw Hill.

Sood A.K. & Enbody, R. (2014, December 19). https://www.georgetownjournalofinternau-s-military-defense-systems-the-anatomy-of-cyber-espionage-by-chinese-hackers. Retrieved from georgetownjournalofinternationalaffairs.org/online-edition: https://www.georgetownjournalofinternationalaffairs.org/online-edition/u-s-military-defense-systems-the-anatomy-of-cyber-espionage-by-chinese-hackers

Stratfor. (2019, October 20). strait-of-hormuz-chokepoints. Retrieved from https://www.stratfor.com: https://www.stratfor.com/sites/default/files/styles/wv_small/public/strait-of-hormuz-chokepoints.jpg?itok=xSgx6Hhi

Tewari, A. (2011). Advanced Control of Aircraft, Spacecraft and Rockets. Chichester, UK: Wiley.

Tsourdos, A. &. (2011). Cooperative Path Planning of Unmanned Aerial Vehicles . Reston, VA: American Institute of Aeronotics and Astronautics, Vol #235.

Wikipedia. (2020, July 26). A* Algorithm. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/A*_search_algorithm

Wiley, R. G. (1993). Electronic Intelligence: The Analysis of Radar Signals, 2nd ed. Norwood, MA: Artech House.

Wilson, M. (2012). The Use of Low-Cost Mobile Radar Systems for Small UAS Sense and Avoid. Sense and Avoid in UAS Research and Applications.

Yu, X. &. (2015). Sense and avoid technologies with applications to unmanned aircraft systems: Review and prospects. Progress in Aerospace Sciences, 74, 152-166.

Yunmonk Son, H. S. (2015, August 12-14). Rocking Drones with Intentional Sound Noise on Gyroscopic Sensors. Proc. 24th Usenix Security Symposium. Washington, DC: USENIX. Retrieved from https://www.usenix.org/conference/usenixsecurity15/technical-sessions/presentation/son

Zhang, Z. W. (2020). Rapid Penetration Path Planning Method for Stealth UAV in Complex Environment with POP-UP Threats. International Journal of Aerospace Engineering, TBA.

Endnotes